목차

해당 포스트(Linear Algebra)는 유투브 혁펜하임의 강의 내용을 듣고 제 생각대로 정리한 내용이라 틀린 내용이 있을 수 도 있습니다.
내적이란?(Dot product)

수식은 위와 같이 간단합니다. 예를 들어 [1 3], [2 4] 벡터의 내적은 위 수식에 따르면 2+12= 14가 됩니다.
내적의 의미에 대해 살펴 보겠습니다.

벡터의 크기를 알려 줄때는 위 수식2와 같이 || || 로 표기 합니다. 위 수식 2는 고등학교때 나오는 수식으로 좌표계에서 임의의 벡터에 대해 그려보면 수식2와 같이 증명이 됨을 알 수 있습니다.

수식2는 수식3으로 설명이 됩니다. x크기에 cosΘ를 곱한 것은 위 그림에서 노란선의 점선과 마주치는 곳까지의 y벡터 값이 됩니다.
즉 내적의 수식을 통해 의미를 살펴 보면 x벡터를 y벡터에 정사영을 내린 값과 y벡터를 값한 값이다. 정사영을 내렸다는 의미는 Projection라는 말로 "투사"하였다는 의미로 x를 y에 투사한 값과 y 값을 곱한 값으로 x와 y가 서로 얼마나 관계되어 있는지를 알 수 있습니다.
두 벡터의 각도 값 Theta Θ가 0일때 두 벡터의 크기는 가장 크게 나올 것이고 90도 일 경우는 0으로 서로 상관 관계가 없다고 합니다. 다른 표현으로 Orthogonal 하다라고 표현합니다.
직교성(Orthogonal)을 가장 잘 표현하는 예가 오일러 지수들과 [1 0], [0 1]과 같이 90도를 이루면서 관계가 없는 벡터 들입니다.
벡터 정규화(Vector Normalization)
벡터를 정규화 한다는 의미는 방향은 변함이 없고 크기를 1로 맞춘다는 의미 입니다. 그리고 Unit Vector라고 불리는 단위 벡터는 크기가 1인 벡터입니다.
즉, 정규화(Normalize)를 진행한 벡터는 단위 벡터가 되는 것입니다.
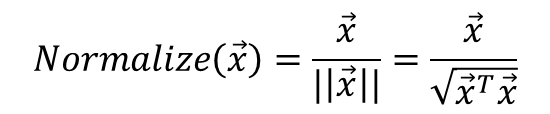
수식으로는 위와 같이 표현 될 수 있습니다.
정사영 수식(Projection Equation) 구하기

위 그림에서 x벡터가 y벡터에 정사영 된 벡터(노란색 화살표)를 구해 보겠습니다.
크기는 수식3에 의해 아래와 같이 표현 될 수 있습니다.

수식5는 벡터 값이 아닌 스칼라(Scalar) 값입니다. 이제 방향 요소를 넣어야 합니다. 방향은 y벡터를 정규화한 유닛 벡터를 곱해주면 됩니다.

수식6이 노란색 벡터를 의미하는 식입니다. 왼쪽이 스칼라로 크기 값이고 오른쪽이 벡터 값으로 방향을 알려 줍니다.