목차

해당 포스트는 유투브 혁펜하임을 통해 공부하여 작성하였습니다.
미분방정식(Homogeneous, Particular, LCCDE)이란?
앞서 포스트에서 왜 미분방정식을 사용하고 현실 세계에서 어떻게 적용되는지에 대해 알아보았습니다. 이번 시간에는 현실 세상(물리, 전자)에서 나오는 미분방정식 형태인 LCCDE(Linear Constant Coefficient Differential Equation)에 대해 알아보고 해당 미분 방정식의 근을 구하는 방법에 대해 알아 보겠습니다.

LCCDE(Linear Constant Coefficient Differential Equation)을 수식으로 전개하면 위와 같습니다. 입력과 출력 값이 미분형태로 표현이 되고 각 미분은 시간에 상관 없는(Constant Coefficient) 계수를 가지고 곱과 더하기로 연결된 선형(Linear) 형태 입니다.
앞서 포스트의 차량 속도와 힘에 대한 입출력이나 전자회로의 전압, 전류 관계가 모두 위 수식에 의해 표현이 됩니다.
미분방정식의 Homogeneous, Particular Solution란?

위와 같이 차의 속도에 대한 미분 방정식이 있다고 생각해보겠습니다. 입력값으로 들어가는 힘x(t)는 지수함수로 표현되어 있다고 생각하겠습니다.
이때 입력에 대한 출력의 근을 구할 때 단순히 입력값만을 생각해서는 안됩니다. 왜냐하면 차에 힘이 들어가지 않은 채로 어떠한 속도를 가지고 있는 상태일 수 있기 때문입니다. 이러한 초기 속도 값을 Auxillary Condition(초기 조건)이라고 합니다.



식(2)은 Homogeneous Solution으로 입력이 없는 상태에서의 속도 출력값(yh(t))에 대한 식입니다.
식(3)은 Particular Solution으로 입력이 들어갔ㅇ르 때의 속도 출력 값(yp(t))입니다.
우리가 알고 싶은 실제 속도는 Homogeneous Solution과 Particular Solution의 합으로 식(4)과 같이 표현 됩니다. 즉, Homogeneous Solution과 Particular Solution을 알아야 실제 출력에 대한 근을 구할 수 있게 되는 것입니다.
미분방정식(LCCDE) 근 구하기 예제
앞서 식(1)에서의 근을 구해 보겠습니다.
우선 식(2)의 Homogeneous Solution을 구해보겠습니다. 식(2)는 출력 y를 미분하고 미분 안한값과 더했을 때 0이므로 출력값 y는 지수 형태임을 알 수 있습니다.

위 식을 식(2)에 대입하면 s=-3으로 나옵니다.

다음은 Particular Solution을 구해보겠습니다.

위와 같이 yp를 대입하고 B를 구하면 B는 1이 나옵니다.
최종적으로 결과는 아래와 같이 나옵니다.
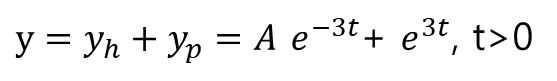
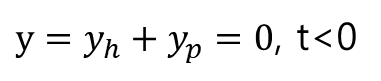
여기에 만일 Auxillary Condition이 y(0)=0 과 같이 주어지면 A값은 -1로 나올 수 있게 됩니다.
'여러가지공부 > 공업수학_신호처리' 카테고리의 다른 글
| 내적, 외적이란?(Inner, Outer Product, vector, scalar) (1) | 2022.11.07 |
|---|---|
| 푸리에 급수란?(수식, 정의, Continuous Time Fourier Series) (0) | 2022.11.06 |
| 미분 방정식을 사용하는 이유? (Why need Differential equation?) (0) | 2022.10.30 |
| [라플라스변환] 변환 공식, Step Function 변환 예제(Laplace, 스텝 함수) (0) | 2022.10.26 |
| [라플라스 변환] Laplace Transform 이란? 기본 개념 익히기 (0) | 2022.10.25 |