라그랑주 보간법, 2 , 3 points 도함수 구하기(미분, derivative, differentiation, Lagrange)

 

목차

 

 

 

 

 

 

도함수(Derivative) 구하기

도함수는 간단하게 함수를 미분하여 나온 미분 함수 입니다. 일반적인 미분법은 2개의 포인트(2 Points)를 사용해서 구합니다. 

2 Points 는 다시 크게 Forward와 Backword로 구분됩니다.

 

 

http://www.multiphysics.us/FDM.html

 

위 그림과 같이 h 값이 양수이고 오른편에서의 기울기를 가져오는 방법이 forward 입니다.

 

수식은 위와 같이 표기 합니다. 

 

 

 

Backward 2 Points는 위 그림에서 왼편에서 시작된 값으로 h가 음수를 사용해서 0에 가깝게 가져와서 기울기를 가져 옵니다. 

 

수식은 위와 같이 표기 합니다.

 

 

 

 

 

 

라그랑주 보간법 , 3 points 도함수 구하기

 

라그랑지 보간법(Lagrange Interpolation)의 수식에 대해 여기서는 상세하게 다루지 않습니다. 다만 3 points 다항식을 구하기 위해 3개의 점에 대해 2차 방정식을 구하는 데에 라그랑지 보간법(Lagrange Interpolation)을 사용합니다. 

 

라그랑지 보간법은 간단하게 몇 개의 포인트가 있을 경우 해당 포인트로 다항식을 만드는 수식입니다. 3points 도함수란 결국 3개의 포인트를 알고 있을 경우 이를 통해 2차 다항식을 라그랑주 보간법으로 만들고 미분하여 가운데 포인트 값을 입력 합니다. 

 

위 수식은 (x0, f(x0)), (x1, f(x1)), (x2, f(x2)) 3개의 포인트를 알면 위와 같이 2차 다항식을 만들 수 있습니다.

 

 

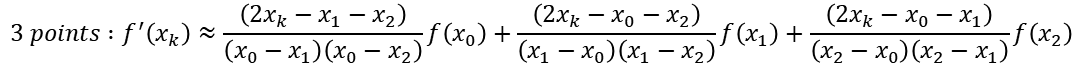
3 point 미분법은 다항식을 미분하고 가운데 포인트 x1을 입력하여 나온 값입니다.