목차

통계 가설 검정, 귀무/대립 가설, 유의수준, p-value란?
가설 검증/검정(Hypothesis Tests)는 말 그대로 가설을 검증하는 이론입니다. 다만 느낌적으로 풀어내는 것이 아닌 수식적으로 풀어내는 것입니다.
예를 들어 동일한 크기의 소리를 발생하는 스피커를 제작 하는 회사가 있다고 가정하겠습니다. 해당 소리 크기는 10 pascal에 맞춰서 나온다고 합니다. 이중에서 샘플 n개를 뽑아서 실제 샘플의 스피커들이 10 pascal에 맞추는지 확인하는 것이 가설 검증이라고 합니다.
검증을 위해 2가지 가설을 세울 수 있습니다.
- 귀무가설(Null Hypothesis) : 반대로 기각하려는 가설 H0
- 대립가설(Alternative Hypothesis) : 증명하려는 가설 H1
가설 검증은 일반적으로 귀무 가설이 틀렸다고 증명하면서 검증을 하는 것입니다. 귀무가설은 일반적으로 H0으로 표기하고 대립가설은 H1로 표기 합니다.
스피커 예제에서 귀무가설은 스피커가 10pascal이 안 나온다는 가설(H0)이 됩니다.


모집단에서 샘플을 취하면 정규분포의 형태를 따릅니다. 샘플의 정규분포는 수식1과 같이 표현할 수 있습니다.

정규 분포(X)는 표준 정규 분포(Z)로 위와 같이 변환이 가능 합니다. 해당 내용에 대해서는 앞서 포스트들에서 설명했으니 참조하시면 됩니다.

수식2의 표준 정규 분포(Standard Normal Distribution)은 그림2와 같이 표현이 가능 합니다. 앞서 포스터에서 신뢰구간(Confidence Interval)을 설명했는데 -1.96~1.96사이 확률 값이 95%였습니다.
유의 수준은 해당 가설을 채택할지 말지의 경계 값입니다. 예를들어 그림2와 같이 1.96을 유의 구간으로 잡으면 내부 면적은 0.95가 되고 빨간선 밖은 0.05가 됩니다. 즉 여기서는 유의 수준을 5%로 잡은 것입니다.
다시 스피커 예를 들면 귀무가설(Null Hypothesis)은 스피커가 10pascal이 안 나온다는 가설(H0)이었습니다. 그리고 유의 수준을 5%로 잡으면 H0은 95% 확률로 틀리게 됩니다. 그래서 H1이 95%의 확률로 성립되게 되는 것입니다.
p-value는 귀무 가설(H0)이 옳다는 전제로 계산되는 확률입니다. 그러므로 유의 수준보다 작을 수록 귀무가설이 틀리게 되므로 p-value는 작을 수록 가설이 성됩니다.
선형회기와 가설검증(Linear Regression and Hypothesis Tests)
앞서 포스트들을 통해 선형 회기에 대해 이해하고 있다는 가정에서 진행하겠습니다.
선형회기란 결국 파라미터 값 베타들을 찾는 모델입니다(https://scribblinganything.tistory.com/690). 여기서 가설 검정이란 모델링한 가설에 대한 검증을 하는 것입니다.

우선 선형회기에서 귀무가설과 대립가설은 아래와 같습니다.
- H0: X와 Y 사이 관계(Relationship)가 없다(β1=0)
- H1: X와 Y 사이 어떤 관계가 있다.(β1≠0)
당연히 수식3에서 β1가 0이 되면 X, Y 사이는 관계가 없어지게 됩니다.
앞서 t 분포 설명 포스트(https://scribblinganything.tistory.com/689)에서 t 분포란 표본 집단(Sample)에서 표본 진단의 분산에 따른 분포라고 설명하였습니다. 해당 포스트의 수식3을 선형회기 베타에 대해 적용을 하면 아래와 같습니다.
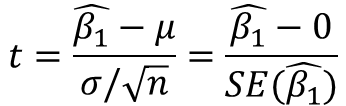
t 값이 커지면 H1이 성립하고 t 값이 작아지면 H0이 성립하는 것입니다. 그리고 p-value는 작을 수록 H1이 성립되고 클수록 H0이 성립됩니다.

즉, t 분포도와 자유도에 의해 확률 그래프가 그려지고 β1가 추정치가 정해지면 해당 값이 포함되는 그래프의 바깥부분의 확률 값이 결정되고 이 확률에 의해 H0의 가설을 수치적으로 검증할 수 있게 됩니다.
'여러가지공부 > 통계적학습(Statistical Learning)' 카테고리의 다른 글
| [Python] Multi Linear Regression 실습 3차원 모델 그리기 (Boston House Price 주택 가격 추정, 다수 선형 회기) (0) | 2023.03.29 |
|---|---|
| 선형회기 R제곱 통계값이란?(Linear Regression, R2, R^2, R Square) (0) | 2023.03.29 |
| 통계 신뢰 구간(Confidence Interval)이란? 선형회기 적용 수식 풀이 (0) | 2023.03.28 |
| 선형회기와 표준 오차(Linear Regression, Standard Error) (0) | 2023.03.25 |
| t 분포란? 자유도 n-1 사용 이유 쉽게 풀이(t-distribution) (0) | 2023.03.25 |