목차

표준 오차(Standard Error)란?
표준 오차를 이해하기 위해서는 기본적인 모집단(Population)과 표본 집단(Sample)에 대한 평균, 분산, 표준 분산에 대해 이해가 필요 합니다. 해당 카테고리에 내용들을 정리해 놓았으니 참조하시길 바랍니다.
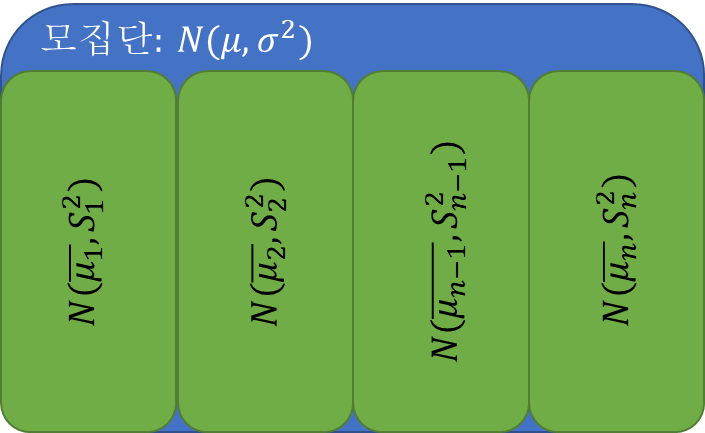
그림과 같이 모집단에서 중복 순열로 샘플들을 뽑아내면 각 샘플에서의 평균을 구할 수 있습니다. 모집단의 평균기호에 바 기호를 붙여서 샘플의 평균 기호를 표기하였습니다.
여기서 샘플들의 평균을 모아서 아래와 같이 평균을 내면 모집단의 평균이 됩니다.


그리고 표본 집단의 평균으로 분선을 구하였더니 수식2와 같이 모집단의 분산에 n으로 나눠준 값이 나왔습니다.
앞서 포스터(https://scribblinganything.tistory.com/687)에서 모집단의 분산은 아래와 같이 구하였습니다.

수식3은 결국 모집단의 데이터 Xi들과 평균의 차이를 구함으로서 편차를 확인하는 것이었습니다.

수식4는 수식2의 분산을 구하는 식을 전개한 것인데 ui는 샘플에 따라 다르기 때문에 추정값입니다. 즉, 추정값이 얼마나 평균에서 떨어져 있는 가를 알려주는 지표기이 때문에 이는 에러 성분을 확인하는 것입니다. 그래서 수식 4를 표준 오차의 제곱으로 표현됩니다. 해당 값에 Square Root를 씌우면 표준 오차(Standard Error)가 됩니다.
선형회기(Linear Regression)에서 표준 오차(SE)란?
선형 회기수식은 아래와 같이 전개 됩니다.

X, Y는 사용자가 이미 알고 있는 데이터 입력과 출력의 값입니다. 베타 값은 절편 값과 기울기 값입니다. 베타 값을 찾는 과정이 선형회기 모델링을 하는 과정입니다.
여기서 잔차 제곱 합(RSS, Residual Sum of Square)라는 개념이 나오는데 이는 베타 파라미터를 구하고 X, Y의 데이터를 넣었을 때 발생하는 에러 정도를 제곱으로 표현 한것입니다.

수식6은 RSS를 구하는 식으로 실제 값에서 추정치 값을 빼서 제곱한 것으로 에러 성분의 크기를 구하는 것입니다. 여기서 삿갓은 추정치 파라미터라는 의미 입니다.
여기서 수식6은 베타들에 대해서 2차 식이기 때문에 Convex 함수입니다.즉, 최저점이 존재하는 그래프입니다. 각 각을 편미분 해서 기울기가 0이 되게 하는 최저점은 아래와 같습니다.


x 바는 평균 값을 의미 합니다. 앞서 수식1~수식4의 바는 추정치 ^ 표기여야 합니다. 혼선 드려서 죄송합니다.
수식5에서 X, Y는 우리가 모은 데이터지만 결국 이 데이터를 사용해서 모델링을 하고 예측을 하려고 합니다. 그 의미는 X, Y는 모집단의 일부 샘플링 값인 표본 집단이 되는 것입니다. 그러므로 수식4와 수식7, 8을 사용해서 베타 파라미터에 대한 SE를 구할 수 있습니다.


여기서 시그마 제곱 값은 수식5에서 모집단의 에러에 의한 분산이므로 아래와 같이 표현 될 수 있습니다.

그리고 샘플에서 생기는 입실론 간에는 Uncorrelated 성질을 가집니다. 그리고 시그마를 RSE(Residual Standard Error)라고 하는데 이는 RSS에서 n-2를 나눈 값에 1/2 제곱한 값입니다. n-2를 나눈 이유는 제 생각에는 RSS식에서 x, y가 서로 correlated 되어서 자유도 2개가 빠진것으로 생각 됩니다.(온전히 제 생각임)
수식9에서 절편 값 베타0은 모집단의 입력 평균 값이 0일 수록 표준 오차가 작아지는 성질을 가집니다. 생각해보면 입력 값이 0을 중심으로 균등하게 퍼지거나 모여 있으면 절편의 값이 오차없이 정해지기 때문입니다.
수식10에서 입력값 xi값이 퍼질 수록 오차가 작아집니다. 이 부분도 상식적으로 생각하면 x 값이 넓게 퍼져 있으면 1차 함수인 기울기 성분이 에러를 적게 반영할 확률이 올라가기 때문입니다.