목차

t 분포(t-distribution)란?
앞서 포스트에서 표본(Sample) 집단에서의 표본 평균, 표본 분산을 구하는 방법에 대해 알아보았습니다. 모(Population) 집단에서 표본 집단을 가지고 표준 정규 분포(Standard Normal Distribution)으로 만들면 아래와 같이 나옵니다.
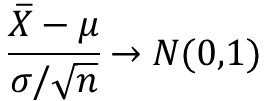
수식1과 같이 X를 표준화하면 표준 정규 분포를 얻을 수 있습니다. 하지만 여기서 문제는 모집단의 표준편차(σ)를 구하기가 힘들다는 것입니다. 표본을 사용하는 이유가 모집단으로 데이터를 다 처리하기 힘들기 때문에 표본을 만든 것이기 때문에 수식1과 같이 모집단의 표준편차를 사용해서 정립하는 것이 현실에 맞지 않기 때문입니다.

그래서 모집단의 표준편차가 아닌 표본 집단의 표준편차(S)를 사용해서 표준화를 적용하는 시도가 일어나게 됩니다. 그리고 이때 어떠한 분포가 생길지에 대한 의미 생겼고 이를 분포도로 정립한 사람이 이를 t-distribution 이라고 명하고 만들게 되었습니다.
t는 학생의 student에서 유래하였다고 합니다. 논문의 저자가 논문에 학생으로 표기하면서 t 분포라고 명명되게 된 것입니다.

t 분포는 수식3과 같이 표기 합니다.
t 분포 자유도(DOF), n-1의 의미?
앞서 수식3에서 n-1이란 자유도(DOF, Degree of Freedom)의 수를 의미 합니다. 만일 샘플의 수가 2개이면 자유도는 1이 되게 되는 것입니다. 물리계에서도 제품의 공진이나 진동 현상을 설명할 때 자유도를 많이 사용 합니다. 제가 생각하는 자유도는 자유도를 가진 요소간에는 독립성을 가진다라고 생각합니다. 즉, A 요소와 B요소가 있을 경우 A요소의 값이 어떻게 변하든 B요소의 값에는 영향이 없는 것입니다.
그럼 관점에서 각 샘플 간에는 각 각의 자유도가 보장되는 것입니다. 즉, n 개의 샘플은 n개의 자유도가 생깁니다.
그럼 t 분포의 자유도는 왜 n-1인가?
수식3을 보시면 t분포는 데이터 뿐 아니라 평균 값 μ를 사용합니다. 평균 값은 샘플의 데이터와 독립된 요소가 아닙니다. 그렇기에 독립된 요소가 하나 빠져야 해서 n-1이라는 값을 사용 합니다.

위 그림은 자유도(ν)에 따른 t 분포도 확률을 그린 그림입니다. 자유도가 무한대로 높아진다는 의미는 샘플의 수가 모분포의 샘플을 다가져다 썼다는 의미이므로 모분포를 표준 분포로 정규화한 N(0,1)에 가까워지게 되는 것입니다.
자유도가 낮아지면 표본에서의 샘플수가 작으므로 샘플에서의 표준편차는 작아집니다. 그러므로 이를 표준화 하게 되면 위 그림처럼 퍼진 종의 형태가 되게 됩니다.

수식4와 같이 t분포를 정의할 수 있습니다. 하지만 이를 적분하는 것은 정규분포를 적분하는 것처럼 쉬운 일이 아니기 때문에 누군가(?) 편하게 테이블로 만들어 놓았습니다.
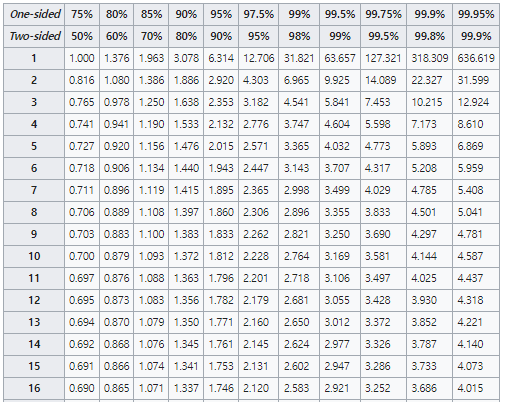
테이블의 일부 값만을 가져 왔습니다. 모든 테이블을 보시려면 위키피디아를 참조 하십시오 행(row) 값이 자유도 입니다.
사용법은 간단합니다.
One-sided를 하면 한쪽 면의 확률만을 적분해서 보겠다는 의미입니다.

위 그림과 같이 빨간선 왼쪽을 모두 적분해서 더하면 0.95가 나오게 되는 것입니다. 테이블 값과 비교해보시길 바랍니다.
'여러가지공부 > 통계적학습(Statistical Learning)' 카테고리의 다른 글
| 통계 신뢰 구간(Confidence Interval)이란? 선형회기 적용 수식 풀이 (0) | 2023.03.28 |
|---|---|
| 선형회기와 표준 오차(Linear Regression, Standard Error) (0) | 2023.03.25 |
| 정규 분포란? 표준화(X, Z값 변환) 쉽게 정리하기(수식, 테이블, Normal Distribution, Standard Distribution) (1) | 2023.03.24 |
| 모집단과 표본집단의 평균,분산,표준편차, n-1로 나누는 이유, 수식 정리(mean, variance, standard deviation) (0) | 2023.03.24 |
| 베이즈 이론(Bayes Theorem)이란? 수식, 사용목적, 쉽게 이해하기 (0) | 2023.03.22 |