목차

통계 신뢰 구간(Confidence Interval)이란?
선형회기에서 신뢰구간(Confidence Interval)이 어떻게 동작하는지 알아보기 전에 통계학에서 신뢰 구간을 어떻게 정의하고 수식으로 전개하는지에 대해 알아보겠습니다.
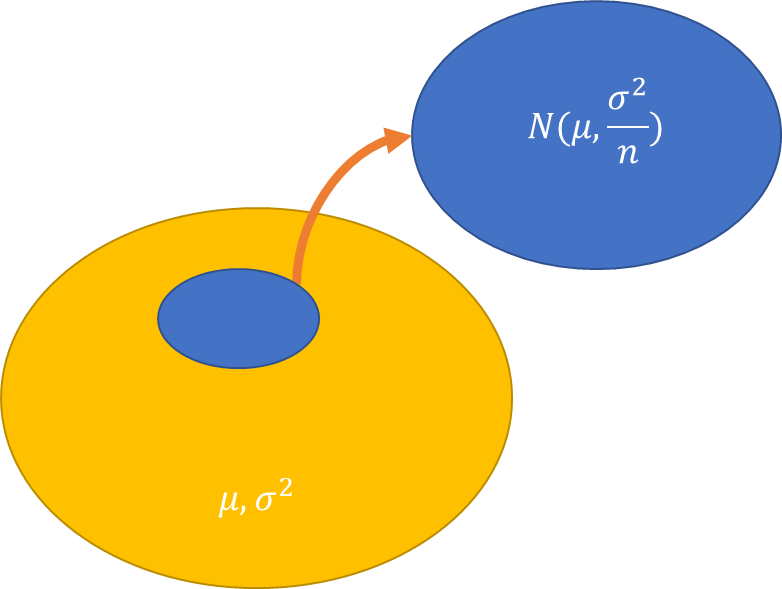
그림1과 같이 모집단(Population)의 평균과 분산이 노란색 박스와 같이 이루어 져있을 경우 모집단에서 일부 샘플 n개를 가져와서 표본집단(Sample)을 만들 경우 해당 표본 집단은 정규분포의 확률 구조를 따른다고 앞서 배웠습니다. 이때 정규분포(Normal Distribution)의 특성을 알려주는 평균과 분산의 값은 그림1의 파란색 박스와 같습니다.

파란색 원의 표준 분포는 수식1과 같이 표기 해줍니다.
신뢰 구간을 얘기 하기 전에 표준 정균 분포(Standard Normal Distribution)에 대해 먼저 얘기 하겠습니다.
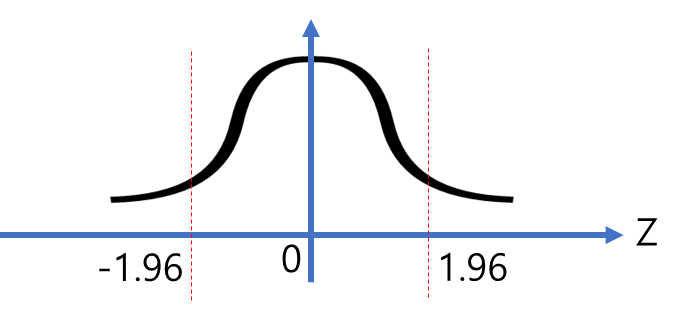
표준 정규 분포는 그림2와 같이 종모양으로 생겼고 종모양 아래 면적이 확률을 의미 합니다. 해당 면적을 일일이 적분하기 힘들어서 누군가(?)가 표준 정규 본포에 대한 적분 값을 확률 테이블로 만들어 놨습니다. 해당 값은 위키피디아(https://ko.wikipedia.org/wiki/%ED%91%9C%EC%A4%80%EC%A0%95%EA%B7%9C%EB%B6%84%ED%8F%AC%ED%91%9C)에서 확인하시면 됩니다.
그림2와 같이 해당 구간의 확률 값은 95%입니다.
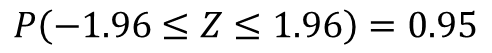
수식2와 같이 표기하는데 의미는 Z값이 -1.96에서 1.96 사이에 값이 나올 확률이 95%라는 의미 입니다. 즉, 신뢰 구간이란 해당 값이 나올 확률에 대해 말하는 것입니다.
앞서 일반 정규 분포(X)를 표준 정규분포로 변환하는 방법에 대해 알아보았습니다(https://scribblinganything.tistory.com/688). 앞서는 X -> Z로 변환했는데 이번에는 Z->X를 수식2에 적용하겠습니다.

수식3과 같이 전개 됩니다. 해당 수식이 신뢰 구간입니다. 모집단의 평균 값이 해당 범위에 있을 확률이 95%라는 의미 입니다. 다른 확률에 대한 값을 알고 싶다면 위 식에서 1.96 부분을 변경하면 됩니다. 해당 값을 k 값이라고 하는데 해당 값에 대한 확률을 테이블로 정리한 것도 있으니 필요 하시면 참조 하시면 됩니다.
선형 회기(Linear Regression)에서의 신뢰 구간 이란?
앞서 선형회기와 표준 오차에 대해 알아보았습니다(https://scribblinganything.tistory.com/690).
표준 오차에서 중요한 수식이 하나 나옵니다.

표준 오류(Standard Error)는 수식4와 같이 표기 되었습니다.

앞서 포스터에서 구한 파라미터의 표준 오차의 위와 같이 나왔습니다.
수식4를 수식3에 적용하면 아래와 같이 우리가 구하는 선형회기 파라미터에 대한 신뢰도를 구할 수 있습니다.

삿갓은 추정치이고 바는 평균 값입니다.