[Python] Multi Linear Regression 실습 3차원 모델 그리기 (Boston House Price 주택 가격 추정, 다수 선형 회기)

여러가지공부/통계적학습(Statistical Learning)

[Python] Multi Linear Regression 실습 3차원 모델 그리기 (Boston House Price 주택 가격 추정, 다수 선형 회기)

끄적끄적아무거나 2023. 3. 29. 08:04

파이썬 Multi Linear Regression 실습 #1

보스톤 주택 가격에 관련된 값들을 서버에서 받아서 dataframe으로 넣어 줍니다.

예제 코드>>

import pandas as pd

df = pd.read_csv('https://raw.githubusercontent.com/rasbt/python-machine-learning-book-3rd-edition/master/ch10/housing.data.txt',
                 header=None,
                 sep='\s+')

df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
print(df.head())

3번 라인: 보스턴 주택 가격 정보 값을 불러서 판다스(Pandas) 데이터 프레임에 넣습니다.

7번 라인: 각 항목에 대한 Column 값을 설정 합니다.

결과>>

      CRIM    ZN  INDUS  CHAS    NOX     RM   AGE     DIS  RAD    TAX  PTRATIO       B  LSTAT  MEDV
0  0.00632  18.0   2.31     0  0.538  6.575  65.2  4.0900    1  296.0     15.3  396.90   4.98  24.0
1  0.02731   0.0   7.07     0  0.469  6.421  78.9  4.9671    2  242.0     17.8  396.90   9.14  21.6
2  0.02729   0.0   7.07     0  0.469  7.185  61.1  4.9671    2  242.0     17.8  392.83   4.03  34.7
3  0.03237   0.0   2.18     0  0.458  6.998  45.8  6.0622    3  222.0     18.7  394.63   2.94  33.4
4  0.06905   0.0   2.18     0  0.458  7.147  54.2  6.0622    3  222.0     18.7  396.90   5.33  36.2

1. CRIM      per capita crime rate by town
2. ZN        proportion of residential land zoned for lots over 25,000 sq.ft.
3. INDUS     proportion of non-retail business acres per town
4. CHAS      Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
5. NOX       nitric oxides concentration (parts per 10 million)
6. RM        average number of rooms per dwelling
7. AGE       proportion of owner-occupied units built prior to 1940
8. DIS       weighted distances to five Boston employment centres
9. RAD       index of accessibility to radial highways
10. TAX      full-value property-tax rate per $10,000
11. PTRATIO  pupil-teacher ratio by town
12. B        1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
13. LSTAT    % lower status of the population
14. MEDV     Median value of owner-occupied homes in $1000s

Column의 정보는 위와 같습니다.

최종 목표는 1~13 사이 값을 사용해서 14번 값을 예측하는 것입니다.

파이썬 Multi Linear Regression 실습 #2

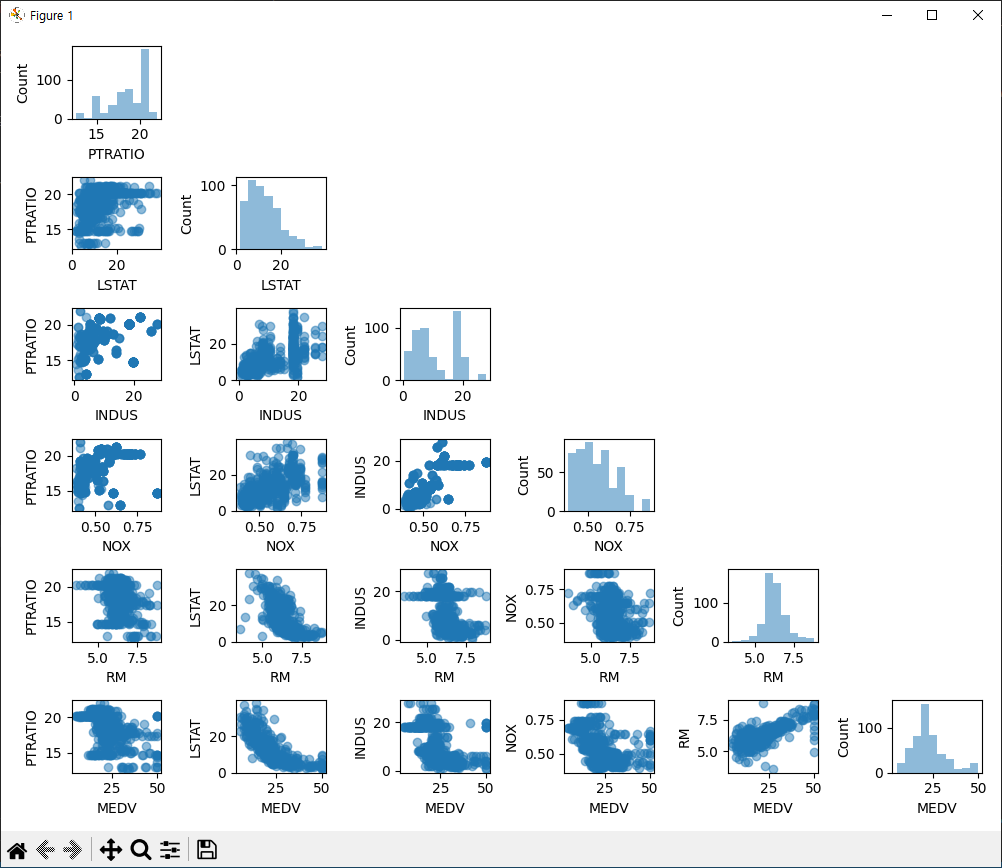
앞서 입력 값 중에 5개와 출력으로 사용할 1개 값을 선택해서 scatter 그래프로 개수를 확인해봅니다.

예제 코드>>

import pandas as pd
import matplotlib.pyplot as plt
from mlxtend.plotting import scatterplotmatrix

df = pd.read_csv('https://raw.githubusercontent.com/rasbt/python-machine-learning-book-3rd-edition/master/ch10/housing.data.txt',
                 header=None,
                 sep='\s+')

df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
plt_cols = ['PTRATIO', 'LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']

scatterplotmatrix(df[plt_cols].values, figsize=(10, 8), names=plt_cols, alpha=0.5)
plt.tight_layout()
plt.show()

10번 라인: matplotlib으로 그려줄 Column 항목들을 리스트로 넣습니다.

11번 라인: scatterplotmatrix 를 사용해서 plt_cols 값들의 scatter 값을 확인합니다.

결과>>

파이썬 Multi Linear Regression 실습 #3

앞서 6개 값의 상관 관계(Correlation)를 확인해봅니다.

예제 코드>>

import pandas as pd
import matplotlib.pyplot as plt

df = pd.read_csv('https://raw.githubusercontent.com/rasbt/python-machine-learning-book-3rd-edition/master/ch10/housing.data.txt',
                 header=None,
                 sep='\s+')

df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
plt_cols = ['PTRATIO', 'LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']

import numpy as np
from mlxtend.plotting import heatmap

print(df[plt_cols].head)
corr_val = np.corrcoef(df[plt_cols].values.T)
corr_map = heatmap(corr_val, row_names=plt_cols, column_names=plt_cols)

plt.show()

15번 라인: corrcoef 함수를 사용해서 plt_cols 값들의 상관계수를 구해줍니다(아래 수식1 참조). 입력 값은 열벡터이므로 전치(Transpose)를 사용해서 행벡터(1xn)로 바꿔 줍니다.

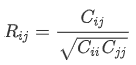
16번 라인: heatmap을 사용해서 상관관계의 크기를 색상으로 표현 해줍니다.

결과>>

<bound method NDFrame.head of      PTRATIO  LSTAT  INDUS    NOX     RM  MEDV
0       15.3   4.98   2.31  0.538  6.575  24.0
1       17.8   9.14   7.07  0.469  6.421  21.6
2       17.8   4.03   7.07  0.469  7.185  34.7
3       18.7   2.94   2.18  0.458  6.998  33.4
4       18.7   5.33   2.18  0.458  7.147  36.2
..       ...    ...    ...    ...    ...   ...
501     21.0   9.67  11.93  0.573  6.593  22.4
502     21.0   9.08  11.93  0.573  6.120  20.6
503     21.0   5.64  11.93  0.573  6.976  23.9
504     21.0   6.48  11.93  0.573  6.794  22.0
505     21.0   7.88  11.93  0.573  6.030  11.9

[506 rows x 6 columns]>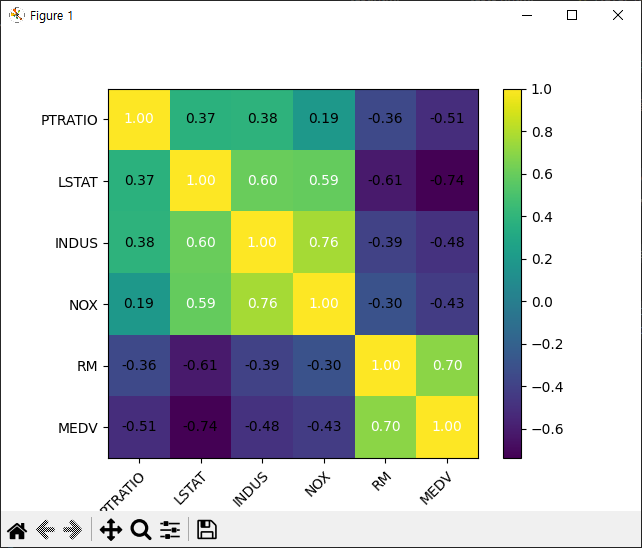

파이썬 Multi Linear Regression 실습 #4

앞서 상관 관계를 통해서 MEDV는 RM와 LSTAT의 상관관계가 높음을 확인하였습니다. RM과 LSTAT을 이용해서 MEDV를 예측하는 모델링을 해보겠습니다.

예제 코드>>

import pandas as pd
import matplotlib.pyplot as plt

df = pd.read_csv('https://raw.githubusercontent.com/rasbt/python-machine-learning-book-3rd-edition/master/ch10/housing.data.txt',
                 header=None,
                 sep='\s+')

df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
plt_cols = ['PTRATIO', 'LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']

X = df[['RM', 'LSTAT']].values
y = df['MEDV'].values

from sklearn.preprocessing import StandardScaler
import numpy as np

sc_x = StandardScaler()
sc_y = StandardScaler()
X_std = sc_x.fit_transform(X)
y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten()


from sklearn.linear_model import LinearRegression

linear_model = LinearRegression()

linear_model.fit(X_std, y_std)
y_pred = linear_model.predict(X_std)

print(linear_model.coef_)
print(linear_model.intercept_)

17~20번 라인: StandardScaler, fit_transform을 사용해서 표준 정규 분포(Standard Normal Distribution)으로 변경해줍니다. 표준 정규 분포와 같은 통계 내용은 앞서 포스트에서 많이 설명하였으니 참조하시면 됩니다.

23~31번 라인: 아래 수식2의 베타 파라미터 값을 구해줍니다. 기울기 값과 절변 값을 sklearn 라이브러리로 수비게 출력 해냅니다.

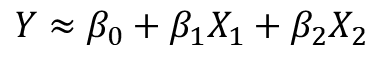
결과>>

[ 0.38921875 -0.49875704]
-6.312906731952e-16

파이썬 Multi Linear Regression 실습 #5

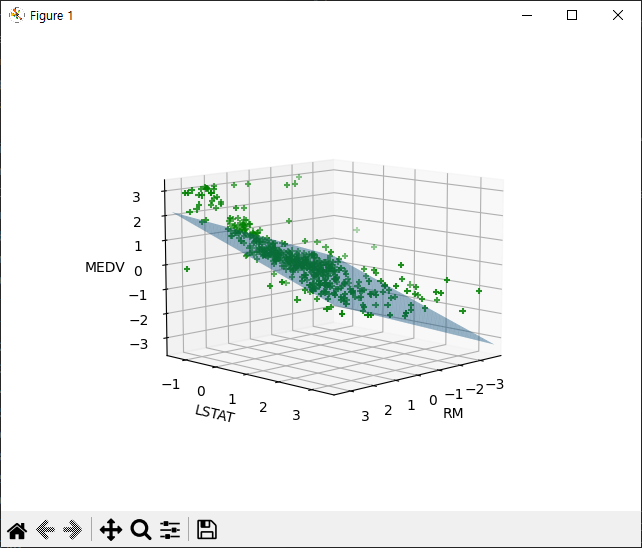
예측된 모델링을 3차원 그래프로 띄우고 실제 값과 비교해서 모델링이 잘되었는지 확인해보겠습니다.

예제 코드>>

import pandas as pd
import matplotlib.pyplot as plt

df = pd.read_csv('https://raw.githubusercontent.com/rasbt/python-machine-learning-book-3rd-edition/master/ch10/housing.data.txt',
                 header=None,
                 sep='\s+')

df.columns = ['CRIM', 'ZN', 'INDUS', 'CHAS', 'NOX', 'RM', 'AGE', 'DIS', 'RAD', 'TAX', 'PTRATIO', 'B', 'LSTAT', 'MEDV']
plt_cols = ['PTRATIO', 'LSTAT', 'INDUS', 'NOX', 'RM', 'MEDV']

X = df[['RM', 'LSTAT']].values
y = df['MEDV'].values

from sklearn.preprocessing import StandardScaler
import numpy as np

sc_x = StandardScaler()
sc_y = StandardScaler()
X_std = sc_x.fit_transform(X)
y_std = sc_y.fit_transform(y[:, np.newaxis]).flatten()


from sklearn.linear_model import LinearRegression

linear_model = LinearRegression()

linear_model.fit(X_std, y_std)
y_pred = linear_model.predict(X_std)

print(linear_model.coef_)
print(linear_model.intercept_)

###그래프###
plt.rcParams['figure.dpi'] = 100

fig = plt.figure()
ax = fig.add_subplot(projection='3d')
ax.view_init(elev=10, azim=45)

xlim = [X_std[:, 0].min(), X_std[:, 0].max()]
ylim = [X_std[:, 1].min(), X_std[:, 1].max()]

xx1 = np.linspace(xlim[0], xlim[1], 100)
xx2 = np.linspace(ylim[0], ylim[1], 100)
xx1, xx2 = np.meshgrid(xx1, xx2)
yy = linear_model.predict(np.stack([xx1.reshape(-1), xx2.reshape(-1)], axis=1))
yy = yy.reshape(100, 100)

ax.plot_surface(xx1, xx2, yy, alpha=0.5)

ax.scatter(X_std[:, 0], X_std[:, 1], y_std, color='green', marker='+')

ax.set_xlabel('RM')
ax.set_ylabel('LSTAT')
ax.set_zlabel('MEDV')

plt.xlim(xlim)
plt.ylim(ylim)
plt.show()

34번 라인: default pixel 사이즈를 설정합니다.

36~38번 라인: 3D 그래프로 그래프를 설정합니다.

40~47번 라인: x1, x2, y 값을 reshape을 사용해서 1차원 배열로 바꾸고 각 성분의 최대 최소 값으로 표현하는 좌표를 설정합니다.

49번 라인: plot_surface 함수를 사용해서 기울기와 절편 값으로 모델링한 평면을 표현 줍니다.

51번 라인: scatter 함수를 사용해서 표준화한 X 값들과 Y 값을 넣어줍니다.

결과>>

저작자표시 비영리 변경금지

'여러가지공부 > 통계적학습(Statistical Learning)' 카테고리의 다른 글

Multinomial Naive Bayes Classifier 수식 및 스팸 메일 예제로 이해하기(Laplace estimator) (0)	2023.04.07
[로지스틱회귀]로짓, 우도, 오즈비 란?(Logit, Log odds, Likelihood function, Logistic Regression) (0)	2023.04.06
선형회기 R제곱 통계값이란?(Linear Regression, R2, R^2, R Square) (0)	2023.03.29
통계 가설검정, 귀무/대립 가설, 유의수준, p-value(Hypothesis Test, Null, Alternative)이란? 선형회기(Linear Regression) 수식 적용 (0)	2023.03.28
통계 신뢰 구간(Confidence Interval)이란? 선형회기 적용 수식 풀이 (0)	2023.03.28

현재글[Python] Multi Linear Regression 실습 3차원 모델 그리기 (Boston House Price 주택 가격 추정, 다수 선형 회기)

파이썬(python), flask, db, coding, 코딩, 주식, IT, 진동, 피로 등 여러가지 공부합니다. 아이와 함께 여행, 맛집 리뷰합니다.

flask, 주식, 플라스크, 부트스트랩, JavaScript, 팜테크, 파이썬, Python, 티킨터, 그래프, Arduino, 함수, 아두이노, 파이선, stress, VR, 변경, c언어, HTML, famtech,

여행하는 코딩끄적끄적