목차

정규분포란(Normal Distribution)?

그림1과 같이 벨 모양과 같이 생긴 형태의 그래프를 정규분포 그래프라고 합니다. 정규분포는 평균값(μ)과 분산(σ^2)에 의해 그래프 특성이 결정 됩니다. 평균에 의해 벨의 중심점이 결정됩니다. 그리고 분산 값에 의해 퍼짐 정도가 결정 됩니다.

그래프의 수식은 위 수식1과 같이 결정 됩니다. 또는 간단하게 아래 수식2와 같이 표현합니다. 평균(Mean)과 분산(Variance)만 있으면 그래프를 그릴 수 있기 때문입니다.

정규분포를 사용하는 이유와 언제 사용 하나?
사실 고등학교때는 무턱대고 위 수식으로 문제를 푸는 것에 집중했지만 사회를 나와서 이과를 다니다 보니 산업의 많은 분야에서 정규분포를 사용함을 알았습니다. 제가 생각하는 정규분포의 이용은 랜덤(Random) 사건에서 필요 합니다.
예를 들어 빗소리 크기를 마이크로폰으로 측정을 하였는데 재미난 사실은 해당 빗소리 크기가 랜덤으로 발생하지만 발생 빈도가 위의 정규 분포를 따른다는 것을 알 수 있었습니다. 이처럼 자연계의 많은 현상들이 정규 분포의 형태를 따릅니다. 이를 통해서 빗소리가 특정 크기까지 발생할 확률을 예측이 가능하게 되는 것입니다.
정규분포와 확률 값(Probability)
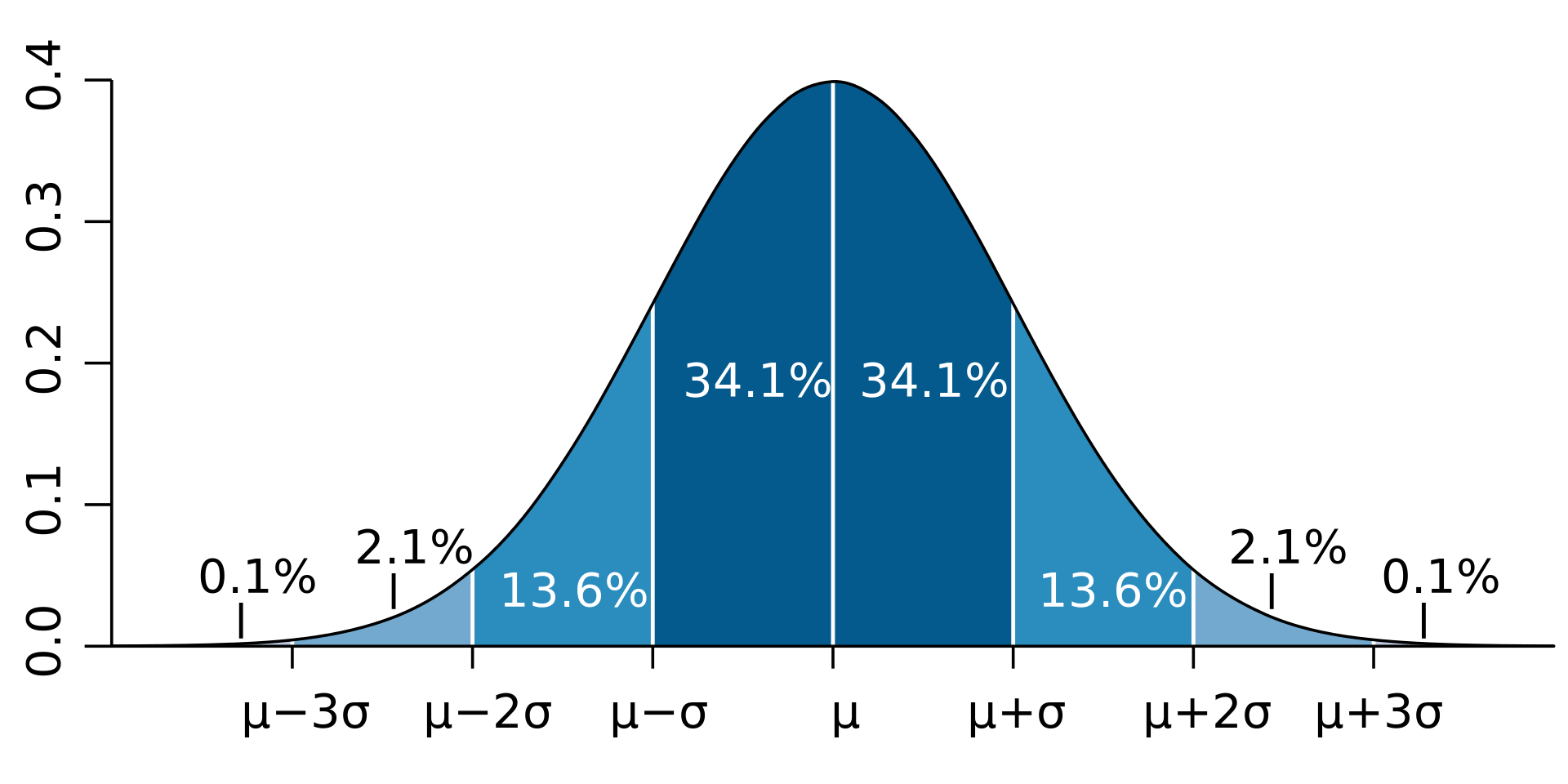
그림2와 같이 평균 값을 중심으로 표준편차(σ) 값에 의해 벨 아래의 면적이 확률 값으로 사용 됩니다. 앞서 비를 예로 들어 설명하면 비의 음압이 5pascal을 평균적으로 발생할 때 표준 편차가 1pascal이면 4~6사이 파스칼이 발생할 확률은 68.2%가 되게 되는 것입니다.
사실 이렇게 면적값을 구할려면 수식1을 적분해야 하지만 누군가(?)가 아래 테이블과 같이 표준편차 값을 사용해서 해당 편차만큼 이동시 발생하는 적분 값을 이미 처리 해놓았습니다.

위와 같이 1시그마 표준편차이면 앞서 말한것과 같이 68.2% 확률로 발생하게 되는 것입니다.
표준 정규분포란(Standard Normal Distribution)?
표준화란 간단하게 말하면 기준이 되는 길이에 맞춰 모든 값들을 비율을 조정하는 것입니다. 표준 정규분포가 나온 이유는 그림1과 같이 다양한 평균과 분산의 정규분포를 평균0, 분산1로 바꾸는 작업입니다. 이렇게 하면 다양한 정규분포를 동일 선상에서 쉽게 확률 값을 비교할 수 있습니다.

그림3과 같이 변환과정을 거치게 됩니다. x값까지의 확률의 면적 값이 표준 정규 분포에서 (x-u)/σ 에서의 확률 면적이 동일하게 됩니다.
일반적으로 확률 범위에 대한 수식을 아래와 같이 표현 해줍니다.

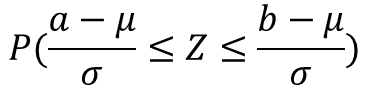
위 두식은 동일한 확률 범위를 가집니다.
'여러가지공부 > 통계적학습(Statistical Learning)' 카테고리의 다른 글
| 선형회기와 표준 오차(Linear Regression, Standard Error) (0) | 2023.03.25 |
|---|---|
| t 분포란? 자유도 n-1 사용 이유 쉽게 풀이(t-distribution) (0) | 2023.03.25 |
| 모집단과 표본집단의 평균,분산,표준편차, n-1로 나누는 이유, 수식 정리(mean, variance, standard deviation) (0) | 2023.03.24 |
| 베이즈 이론(Bayes Theorem)이란? 수식, 사용목적, 쉽게 이해하기 (0) | 2023.03.22 |
| 마르코브(Markov Chain) 체인이란? 파이썬(Python) 예제 실습 (0) | 2023.03.20 |