반응형

모집단(Population)과 표본집단(Sample) 수식 정리
- 모집단/표본집단 평균(Population / Sample Mean)


- 모집단/표본집단 분산(Population / Sample Variance)


- 모집단/표본집단 표준편차(Population / Sample Standard Deviation)


모집단이란 실제 가지고 있는 모든 데이터 샘플을 의미 합니다. 표본 집단은 모집단 중에 일부를 샘플로 취해서 모집단의 평균, 분산, 표준 분산을 추정하는 목적으로 사용 됩니다.
표본집단(Sample) n-1 샘플로 나누는 이유
우선 수식을 떠나서 개념적으로 쉽게 이해해보도록 하겠습니다.
표본 집단을 사용하는 사용자가 N개의 모집단 데이터에서 n개의 샘플을 가져온다고 생각해보겠습니다. 여기서 우리는 평균과 분산에서 경향을 확인할 수 있습니다. 우선 표본 집단 평균은 모집단의 평균 값을 중심으로 나옵니다. 하지만 분산의 경우 모집단의 분산보다 작은 값으로 나옵니다.
위와 같은 현상이 나오는 이유는 논리적으로 생각해보면 분산이란 평균값에서 퍼진 정도를 알려주는 지표인데 표본 집단의 평균은 모집단과 유사하게 나오는 데 샘플의 수 n 는 모집단에 데이터 수 N에 비해 작기 때문에 퍼지는 정도가 클 수 가 없습니다.
위 개념을 실제 수학적으로 적용한 개념이 아래와 같습니다.
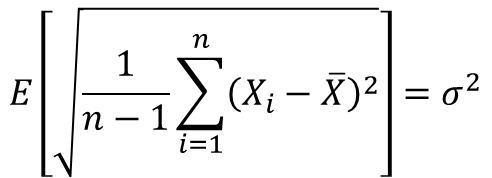
수식1과 같이 기대값을 적용해서 계산을 하니 n-1로 나누었을 경우 표본집단의 분산에 대한 기대 값이 모집단의 분산값으로 나왔습니다.
반응형
'여러가지공부 > 통계적학습(Statistical Learning)' 카테고리의 다른 글
| t 분포란? 자유도 n-1 사용 이유 쉽게 풀이(t-distribution) (0) | 2023.03.25 |
|---|---|
| 정규 분포란? 표준화(X, Z값 변환) 쉽게 정리하기(수식, 테이블, Normal Distribution, Standard Distribution) (1) | 2023.03.24 |
| 베이즈 이론(Bayes Theorem)이란? 수식, 사용목적, 쉽게 이해하기 (0) | 2023.03.22 |
| 마르코브(Markov Chain) 체인이란? 파이썬(Python) 예제 실습 (0) | 2023.03.20 |
| 공분산, 상관 계수, 정규화, Cross correlation, Convolution, Coherence란? 비교 분석(통계, 신호처리) (0) | 2022.12.19 |