[선형대수학] 행렬의 Rank란? (Matrix)

 

해당 포스트(Linear Algebra)는 유투브 혁펜하임의 강의 내용을 듣고 제 생각대로 정리한 내용이라 틀린 내용이 있을 수 도 있습니다.
 
 
 
 

[선형대수학] 행렬의 Rank란? (Matrix)

행렬에서 rank의 의미는 행렬이 가지는 독립적인 Column이나 Row의 수를 의미 합니다. 독립(Independent)의 의미는 https://scribblinganything.tistory.com/676 포스트를 통해 참조 하시면 됩니다.
 
독립적인 벡터가 결국 표현할 수 있는 차원의 수를 의미 했습니다. 그렇기 때문에 독립적인 Column의 수는 Rank이고 Rank의 개수가 Column Space를 표현하는 차원의 수를 의미 합니다. 
 
예를 들어 알아보겠습니다. 
 

수식1

 
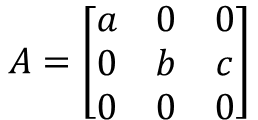
위 수식1의 독립 Column 벡터의 수는 앞서 포스트에 따라 총 2개로 나올 수 있습니다. 그러므로 Rank의 수는 2개가 되고 표현할 수 있는 Column의 차원은 2차원이 되는 것입니다. 
 
비록 A는 3 x 3으로 3차원까지 표현이 가능한 행렬(Matrix)이지만 Rank의 한계로 실제로는 2차원 평면에 대해서만 값을 표현할 수 있습니다. 
 
 
 
 
 

[선형대수학] Rank의 분류

 
랭크는 아래와 같이 분류 할 수 있습니다. 
 
 

• Full Rank

n x n 행렬에서 rank 값이 n 인 경우
 
 

• Full Row Rank

n x m 행렬에서 rank 값이 n 인 경우
 
 

• Full Column Rank

n x m 행렬에서 rank 값이 m 인 경우
 
 

• Rank Deficient

n x m 행렬에서 rank 값이 min(n,m)보다 작은 경우