목차

해당 포스트는 유투브 혁펜하임을 참조해서 작성하였습니다.
Z 변환(Z Transform)이란? 수식 풀이
Z변환이란 앞서 라플라스 변환을 연속이 아닌 이산/불연속(Discrete)에서 처리하는 변환 방식입니다. 앞서 포스트에서 라플라스(Laplace) 변환은 기본 함수에서 시그마 지수가 포함된 값을 넣어서 해당 전달함수가 수렴되는 영역(ROC, Regions of Convergence)을 찾았습니다.
이와 마찬가지로 Z변환도 일반 이산 주파수 변환에서 아래와 같이 r^(-n)을 넣어서 수렴 영역을 찾아 줍니다.

Z변환은 위와 같이 기존의 이산 푸리에 변환에서 오메가 변수 이외에 r이라는 변수를 가지는 변환입니다.
r과 Ω 를 아래와 같이 정의를 합니다.

수식2를 수식1에 정의해서 Z 변환 수식을 아래와 같이 정리 합니다.

Z 도메인이란?(Z Domain)

앞서 수식2에서 Z에 대한 정의를 위와 같이 하였습니다. Z를 2차원 평면에 표현할 경우 r는 지름으로 동작하고 Ω는 회전 각을 의미할 수 있습니다.

위 그림과 같이 Z를 Real과 Imaginary로 구분하여 표현한 것을 Z 도메인이라고 합니다. 그리고 r 값이 결정되면 해당 원을 따라서 푸리에 변환 값이 나오게 되는 것입니다.

위 그림이 원을 따라 나오는 주파수 값을 표현한 예제입니다. 참조만 하시길 바랍니다.
Z변환에서의 ROC
ROC를 예제를 통해 설명하겠습니다. ROC는 앞서 라플라스 변환에서 설명한 것과 같이 해당 수식이 수렴하게 만드는 영역입니다.

위 수식4를 Z 변환하면 아래와 같습니다.

위 적분의 의미는 아래 조건이 만족해야 X(Z)가 수렴하게 됩니다.
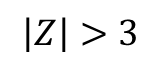
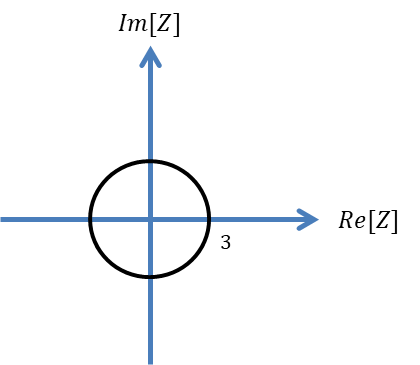
즉 Z domain에서 원 영역 밖에 위치해야 ROC 의 영역이 됩니다.
'여러가지공부 > 공업수학_신호처리' 카테고리의 다른 글
| 라플라스 변환이란? 사용 이유와 ROC(Region of Convergence), a+bj (2) | 2023.02.04 |
|---|---|
| DFT(이산 푸리에 변환) 매트릭스, FFT, Cyclic Convolution (0) | 2023.01.08 |
| 주파수 분석장치의 이산 푸리에 변환(DFT, Discrete Fourier Transform)의 수식과 정의 (0) | 2023.01.03 |
| 이산 시간 푸리에 변환 수식 전개하기(Discrete Time Fourier Transform) (0) | 2022.12.29 |
| 이산 시간 푸리에 시리즈란? 계수 값 유도하기(Discrete Time Fourier Series, ak, DTFS) (2) | 2022.12.27 |