
해당 포스트는 유투브 혁펜하임을 참조해서 작성하였습니다.
DFT Matrix(이산 푸리에 변환 매트릭스)
앞서 포스트에서 DFT(Discrete Fourier Transform) 전개에 대해 알아보았습니다(https://scribblinganything.tistory.com/653).

위 수식(1)에서 3개의 포인트 입력 값을 넣고 3개의 출력 값을 받는 형식을 행렬(matrix)로 만들어 보겠습니다. 3개의 입출력은 k=0, 1, 2 로 생각할 수 있습니다.

수식(1)을 3개의 입출력으로 행렬로 표현하면 위와 같습니다.
Orthogonal Matrix 는 Orthonormal 한 벡터(Vector) 값을 Column으로 가지는 행렬을 의미합니다. 즉, 크기는 1로 만들고 서로 직교성을 가지게 만들어야 합니다. 오일러 지수는 서로 직교성을 가짐을 예전에 증명하였으므로 크기를 1로 만드는 작업을 해야 합니다.

수식(3)과 같이 나눠 주면 Unitary Matrix가 됩니다. 여기서 N은 3입니다.
유니타리 행렬은 아래의 특성에 의해 역 DFT가 쉽습니다.

해당 특징은 선형대수에서 확인하시길 바랍니다.
즉, 최종적으로 아래와 같이 정리됩니다.


FFT(Fast Fourier Transform)란?
앞서 DFT 행렬에서 알 수 있듯이 DFT는 매트릭스 안의 행과 열의 수만큼 계산을 진행해야 합니다.
만일 NxN 행렬이면 N^2 만큼의 계산을 처리해야하는데 FFT(Fast Fourier Transform)은 해당 행렬을 쪼개서 병렬로 처리해서 N^2 계산 속도가 걸리는 것이 아닌 NlogN의 속도로 줄여줘서 빠르게 처리한다고 해서 FFT라고 불립니다.
Cyclic Convolution이란?
기존에 CTFT, DTFT 푸리에 변환에서 Convolution 곱을 푸리에 변환하면 주파수에서의 곱으로 쉽게 표현할 수 있음을 확인했었습니다.

Cyclic Convolution은 DFT에서 사용되는 개념입니다. 아래와 같이 Cyclic Convolution을 한 식을 DFT 주파수 변환을 하면 단순 곱으로 표현할 수 있습니다.

Cyclic Convolution이 Convolution과 다른점은 아래와 같이 주기를 가지는 x, h 신호를 컨볼루션하게 되면 적분값이 수렴이 되지 않고 발산(공진, Resonance)을 하게 되기 때문에 사이클릭 콘볼루젼은 한번의 주기에 대한 적분만을 진행합니다.
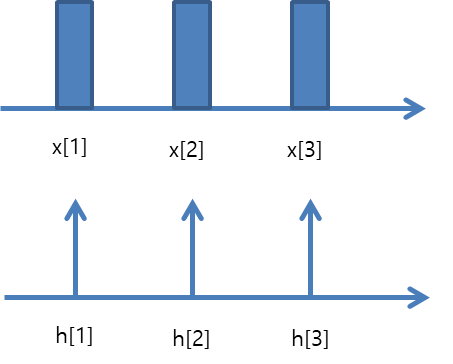
Cyclic Convolution 은 위와 같은 그림에서 h(n)의 한주기만 남기고 x[n]과 컨볼루션 하는 것입니다. DFT도 결국 N개의 입력을 가져와서 N개의 출력을 가져오기 때문에 한개의 주기를 가져와도 괜찮습니다.
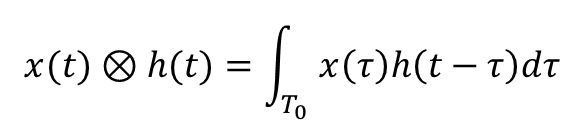
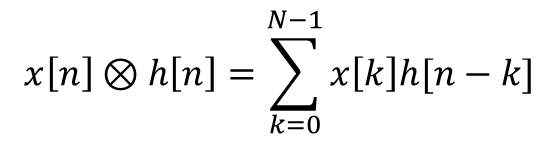
사이클릭 컨볼루젼은 위와 같이 기존의 컨볼루션이 전 구역을 적분하였지만 T0라는 하나의 주기에 대해서만 적분을 합니다.
FFT 주파수 범위와 주파수 정밀도
FFT(Fast Fourier Transform)은 알고리즘 적으로 DFT를 빠르게 한 방식으로 DFT로 설명하면 됩니다.

앞서 수식(2)에서 x[n]이 특정 주파수를 가지는 아래와 같은 신호로 생각해보겠습니다.
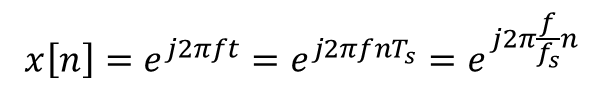
x[n]을 수식(2)에 넣으면 아래의 경우가 아닌 경우 내적의 합이 0이 됩니다. 그러므로 Xk의 값을 지니는 부분은 아래 수식(4)를 만족해야하는 것입니다.

즉, 수식(4)를 통해 수식(5)가 완성됩니다.
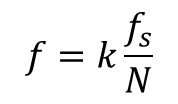
k = 0, 1, 2 의 의미는 0Hz, fs/N Hz 2fs/N Hz가 되는 것입니다.
'여러가지공부 > 공업수학_신호처리' 카테고리의 다른 글
| Z 변환이란? (ROC, 수식 유도, Transform,Z-Domain, 라플라스 차이) (0) | 2023.02.05 |
|---|---|
| 라플라스 변환이란? 사용 이유와 ROC(Region of Convergence), a+bj (2) | 2023.02.04 |
| 주파수 분석장치의 이산 푸리에 변환(DFT, Discrete Fourier Transform)의 수식과 정의 (0) | 2023.01.03 |
| 이산 시간 푸리에 변환 수식 전개하기(Discrete Time Fourier Transform) (0) | 2022.12.29 |
| 이산 시간 푸리에 시리즈란? 계수 값 유도하기(Discrete Time Fourier Series, ak, DTFS) (2) | 2022.12.27 |