진동에서 변위,속도,가속도의 관계
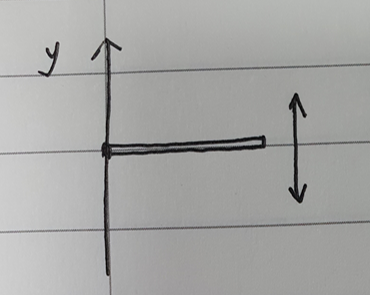
그림1과 같이 고정된 축이 흔들릴 경우 y축의 시간에 따른 움직임은 사인파(Sine wave)이다. 즉, 변위(Displacement)에 대한 파형을 알 수 있으면 시간에 따른 미분으로 속도(Velocity), 가속도(Acceleration)의 파형도 그릴 수 있다. 반대로 가속도를 알 수 있으면 적분으로 나머지 변위와 속도에 대한 정보를 얻을 수 있다.
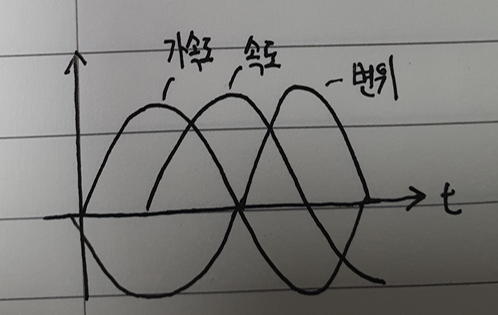
사인파에서 가속도, 속도, 변위의 차이는 위상(Phase)이다. 진동(vibration)에서 가속도, 속도, 변위의 위상 관계는 중요하지 않다. 주파수 영역에서 가속도, 속도, 변위의 진폭(amplitude)가 변하는 데 이 점을 유의 해야한다.
예제를 통해 진동에서 변위,속도,가속도의 관계 이해하기
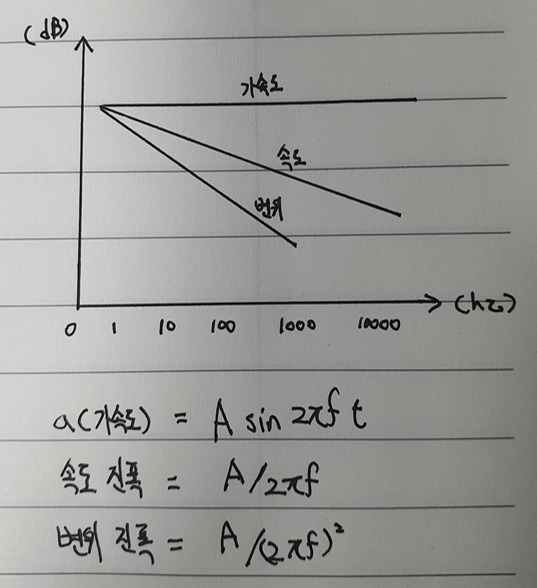
가속도센서(Accelometer)를 이용해서 어느 지점에서 가속도를 측정하였고 사인파를 측정하였다고 가정하자. 그림3은 사인 성분은 제거하고 진폭만을 고려한 그래프이다. 가속도의 진폭(Amplitude)는 A이고 속도는 적분하여 A/(2pi*f) 이고 변위는 A/(2pi*f)^2 이다.
그림3은 관계를 설명하기 위해 극단적으로 그린 그래프이고 사인파에서 발생하는 주파수 성분까지 고려한 표준에서는 아래과 같이 3가지로 분류해서 구분한다.
- 0 ~ 10Hz 영역
- 변위(Displacement) 진폭이 가장 두드러지는 영역
- 느리고 눈으로 인지 가능 (Slow, Visible)
- 적용 분야 : Surging, Water hummer, Ground vibration, Piping vibration
- 10 ~ 100Hz 영역
- 속도(Velocity) 진폭이 가장 두드러지는 영역
- 감도로 인지 가능 (Sensible by touching)
- 적용 분야 : Imbalance, Misalignment, Miscoupling, Bearing defect
- 1kHz 이상 영역
- 가속도(Acceleration) 진폭이 가장 두드러지는 영역
- 소음으로 감지
- 적용 분야 : Bearing damage, Abnormal noise
진동에서 변위,속도,가속도의 관계 수식(Equation)
앞서 그림3의 수식으로 부터 주파수에 따른 가속도, 속도, 변위의 관계 수식을 도출 할 수 있다.
사인파 진동(Sinusoidal Vibration)에서의 수식
V = π * f * D
여기서 D는 변위의 최대폭(Peak to Peak) 값이고 V는 속도의 최대값(Peak) 이다.
A = 2* (π * f)^2 * D
여기서 D는 변위의 최대폭(Peak to Peak) 값이고 A는 가속도의 최대값(Peak) 이다.
G = (2* (π * f)^2 / 9.81 ) * D
여기서 D는 변위의 최대폭(Peak to Peak) 값이고 G는 중력 가속도의 최대값(Peak) 이다.
위 식을 미터법(Metric)으로 계산하면 아래와 같다.
G = 2.013 * (f^2) * D
위 식을 인치(inch)로 계산하면 아래와 같다.
G = 0.0511 * (f^2) * D, 1m = 39.37inch
'여러가지공부' 카테고리의 다른 글
| 사인 스윕파(Sine Sweep)의 사이클(Cycle) 계산 방법(Calculation) (0) | 2021.05.06 |
|---|---|
| 랜덤 진동 이란? (Random Vibration Testing)? (2) | 2021.05.04 |
| Autocorrelation 과 Crosscorrelation 이란(어디에 쓰일까?) (0) | 2021.04.16 |
| SRS (Shock Response Spectrum) 이란? (0) | 2021.04.13 |
| PSD(Power Spectral Density) vs Autopower 비교 (0) | 2021.04.12 |