사인 스윕이란? 그리고 사이클 갯수가 필요한 이유
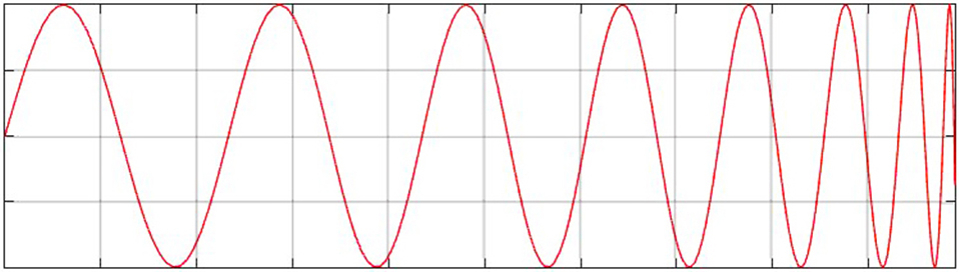
Sinusoidal Sweep wave, 사이파는 그림1처럼 시간이 흐름에 따라서 사인파의 주파수가 변경된다. 즉, 주파수가 시간에 연계되어 변하는 것이다. 주파수 변경 방법은 아래와 같이 2가지 방법이 있다.
- 선형적(Linear) 사인 sweep wave : 주파수가 시간에 비례해서 증가한다.
- 대수적(Logarithmic) 사인 sweep wave : 주파수가 시간에 지수적으로 비례해서 증가한다.
Sine sweep 파형은 시험 규격에서 종종 나오는데 Sine sweep으로 진동이나 시험을 진행하여 몇 번의 싸이클(Cycle)로 시편에 힘을 가했는지에 따라 피로도(Fatigue)나 내구성(Durability)를 확인할 수 있다. 일반 사인파의 경우 사이클은 주파수에 비례하므로 쉽게 구할 수 있지만 sweep 파형의 경우 별도의 계산 방식이 필요 하다.
Linear Sine Sweep Cycle Calculation (선형 사인 스윕파 사이클 계산법)
f1(Hz)에서 f2(Hz) 로 v(Hz/min)의 속도로 주파수가 증가하는 Sweep 파형의 1번 Sweep 시 발생하는 사이클(Cycle) 총 수는?

그림2에서 x축은 시간 y축은 주파수이다. 이번 문제에서 시간에 따른 주파수는 선형적으로 변하므로 그림2처럼 직선으로 증가한다. 사이클의 총 수는(The number of cycle) 그래프 t0까지의 아래 면적이다. 왜냐하면 주파수(f) = 사이클수(N) / 시간(t) 이기 때문이다.
면적은 아래 사각형 부분과 위 삼각형을 각 각 구해서 더하면 된다.

그림3은 주파수의 속도를 구하는 식이다. t0까지 주파수 변화량을 시간으로 나누면 된다. 속도를 알고 있다면 t0 값을 알 수 있게 된다.

N은 The number of cycle 이다. 그림4는 면적을 구하는 식이다. 마지막에 60초를 곱한 이유는 앞서 가정은 분(minute)로 설정한 속도이기 때문이다. 그림4를 통해 주파수(frequency) 와 Sweep 속도(velocity) 만 알고 있다면 사이클 수를 알 수 있다.
Logarithmic Sine Sweep Cycle Calculation (대수 사인 스윕파 사이클 계산법)
f1(Hz)에서 f2(Hz) 로 v(Octave/min)의 속도로 주파수가 증가하는 Sweep 파형의 1번 Sweep 시 발생하는 사이클(Cycle) 총 수는?
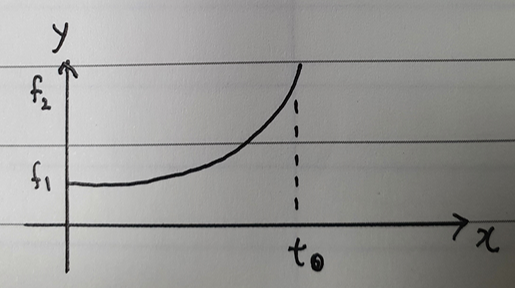
앞서 선형과 다르게 지수적으로 주파수가 증가한다. 여기서 Octave(옥타브)는 2의 배수로 증가한다는 의미로 만일 1Octave로 1Hz부터 증가하면 다음은 2, 4, 8, 16 순서로 주파수가 증가하고 2Octave로 1Hz부터 증가하면 4, 16, 64 로 증가하는 것이다.

그림6은 f1~f2의 Octave 값을 t0로 나눈 값으로 속도가 된다. 해당 식을 통해 t0의 값을 구할 수 있다.
그림5의 그래프를 수식으로 표현하면 2^(v * x) 이다. Ocatave 로 주파수가 증가하는 것은 결국 지수로 증가한다는 의미이기 때문이다.
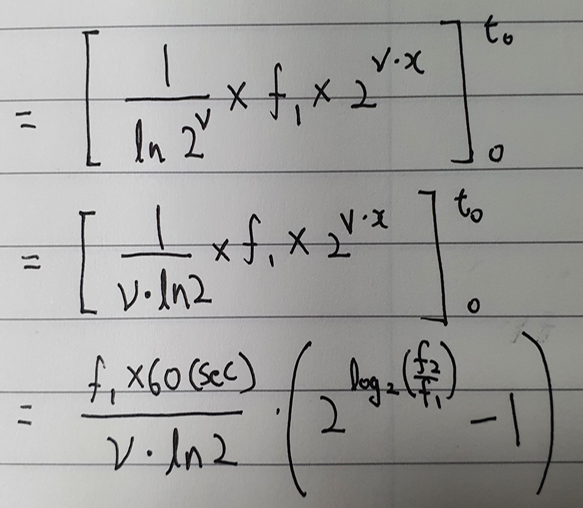
그림5의 그래프를 적분하면 그림7과 같은 식이 나온다.
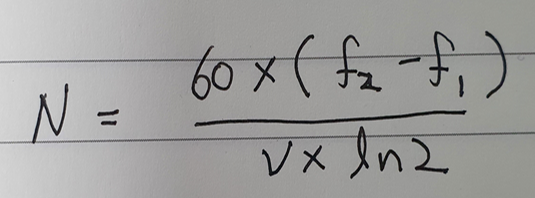
최종 The number of cycle은 그림7의 식을 전개하여 그림8과 같이 쉽게 구할 수 있다. 대수적 사인스윕파도 주파수 범위와 속도를 알면 사이클 갯수를 그림8의 수식으로 구할 수 있다.
'여러가지공부' 카테고리의 다른 글
| Nyquist Plot 이란? (파이썬으로 그리기 예제 포함) (0) | 2021.05.11 |
|---|---|
| Bode Plot 이란? 사용 방법과 그리는 방법, 파이썬을 사용하여 그래프 검증 (0) | 2021.05.10 |
| 랜덤 진동 이란? (Random Vibration Testing)? (2) | 2021.05.04 |
| 진동에서 변위,속도,가속도의 관계 (Vibration, Displacement, Velocity, Acceleration) (0) | 2021.05.04 |
| Autocorrelation 과 Crosscorrelation 이란(어디에 쓰일까?) (0) | 2021.04.16 |