목차

[머신러닝] Covariance란?

그림1과 같이 한반에 학생에 대한 몸무게에 대한 샘플 값들을 위와 같이 가져왔다고 가정하겠습니다. 이때 평균을 x에 바로 표기된 점이라고 하면 샘플의 분산(Variance)는 아래와 같이 구할 수 있습니다.

분산이란 결국 평균 값에서 어느정도 벗어났는지를 계산하는 것입니다. 샘플의 분산 수식이 위와 같이 나오는 이유는 아래 링크에 자세하게 설명하였으니 참조하시길 바랍니다(https://scribblinganything.tistory.com/687).
이번에는 동일 학생으로 부터 키를 측정했다고 생각해보겠습니다. 이때 몸무게와 키의 측정 값으로 부터 유의미한 분석값이 있지 않을까 하는 고민에서 발생한 개념이 공분산(Covariance)입니다.


공분산은 수식1과 같이 표현하고 그림2와 같이 두 데이터 간의 관계를 설명합니다.
공분산은 총 3가지 종류로 정리가 됩니다.
1. Positive Trend(Relation)
2. Negative Trend(Relation)
3. No Trend(Relation)
위 그림처럼 기울기가 양수인 형태는 Positive Trend이고 음수인 경우는 Negative Trend입니다. 그리고 둘 사이 관련이 없을 경우 No Trend 입니다.
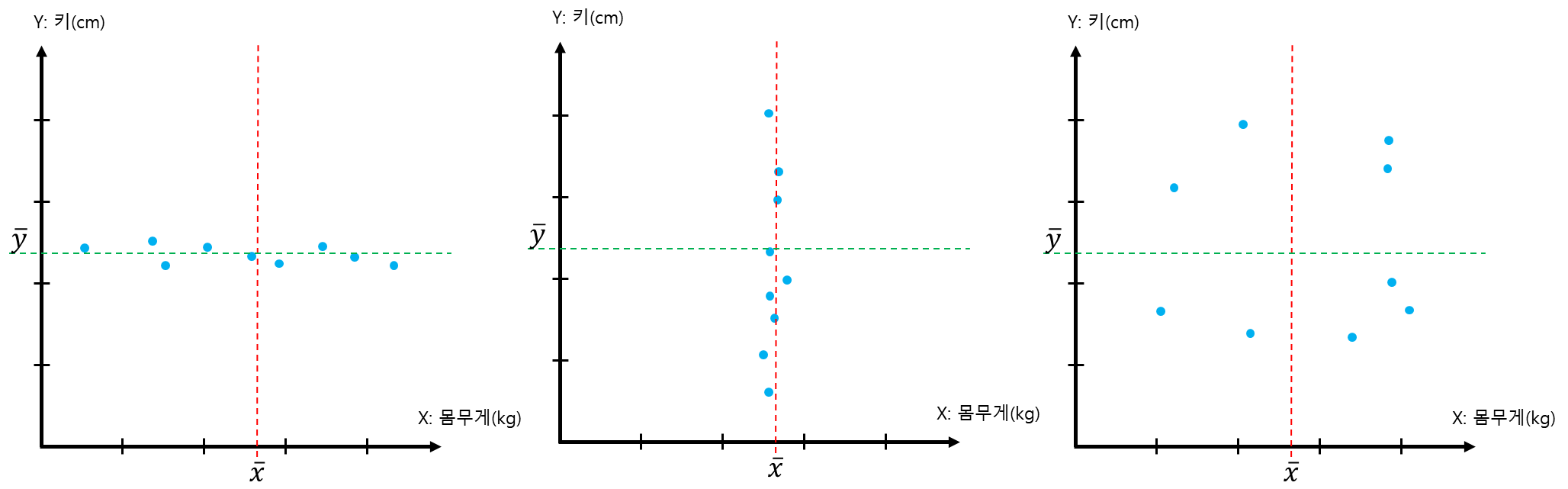
위 그림3과 같이 데이터가 퍼지거나 기울기가 없는 경우 No Trend 입니다.
[머신러닝] Covariance 특징 및 사용 목적


다시 그림2와 수식1을 통해서 설명해보겠습니다. 위 그림에서 평균의 선에 의해서 데이터가 4분면으로 나눠 집니다. 왼쪽 하단의 데이터에 x, y 평균을 빼서 곱하면 양수 값이 그리고 우측 상단도 양수가 나옵니다. 나머지 분면은 음수가 나옵니다. 이러한 특징에 의해 평균 대비 어느 분면에 배치가 많이 되어있는지 합을 통해 기울기가 양수이냐 음수이냐의 트렌드가 나옵니다.
그리고 Trend가 없는 경우는 앞서 그림3과 같이 평균 대비 차이가 없는 값이나 다 퍼져있어서 전체 총합이 0에 가까운 값으로 나옵니다.
이러한 특성에 의해 공분산은 아래와 같은 특성을 가집니다.
1. 공분산을 통해서 Postive, Negative, No trend의 관계를 확인할 수 있다.
2. 공분산의 결과 값 Cov[X,Y]의 크기를 통해서 공분산 정도가 크다라고 판단할 수는 없다.
3. 공분산 자체의 의미는 중요하지 않고 Correlation을 계산하기 위한 단계로 사용된다.
1번의 특성은 앞서 설명을 통해서 이해를 하였다고 생각이 듭니다. 2번 특성은 예를 들면 쉽게 이해할 수 있습니다.
앞서 그림2의 키와 몸무게 샘플값에 각 각에 2배를 곱했다고 생각해보겠습니다. 2배의 값을 곱했지만 키와 몸무게 사이의 관계는 변화가 없습니다. 데이터 샘플의 위치나 기울기는 동일하기 때문입니다. 하지만 수식1에 적용을 해보면 Covariance의 크기가 증가함을 알 수 있습니다. 즉, Covariance의 크기로 두 데이터 간의 관계를 파악하기는 힘듭니다.
3번 특성은 다음 포스트의 Correlation에서 추가 설명 드리겠습니다.
'여러가지공부 > 머신러닝(Machine Learning)' 카테고리의 다른 글
| [머신러닝]SVM(Support Vector Machines)이란? 예제와 수식풀이 (0) | 2023.05.17 |
|---|---|
| [머신러닝]Correlation이란? Covariance 차이, 수식, 사용 목적(피어슨 상관관계) (0) | 2023.05.16 |
| [머신러닝] 랜덤포레스트란? 쉬운예제로 이해하기(Random Forest, Bagging, Bootstrap) (0) | 2023.05.08 |
| [머신러닝]Regression Tree 가지치기(Prune) 예제로 쉽게 이해하기(Cost Complexity/Weakest Link Prunning) (0) | 2023.05.07 |
| [머신러닝] Regression Tree란? 예제로 쉽게 이해하기 (0) | 2023.05.05 |