목차

Bayes’ Theorem
베에즈 이론에 대해 알아보겠습니다.

- P(A|B) : Posterior
- P(A) : Prior
- P(B|A) : Likelihood
- P(B) : Normalizing Constant
Bayes 이론은 사전 확률(prior probability)과 사후 확률(posterior probability)을 사용하여 어떤 사건이 발생할 확률을 계산합니다. 사전 확률은 사건이 발생하기 전에 이미 알고 있는 정보를 바탕으로 계산되며, 사후 확률은 사건이 발생한 후 추가 정보를 토대로 계산됩니다.
간단히 말하자면 training data set으로 P(A|B)와 P(B)를 알아내고 P(B|A)를 구하는 것입니다.

구하고자 하는 값은 위와 같습니다. 해당 값이 무엇인지는 아래 예제를 한번 해보시면 쉽게 이해 되실 겁니다.
Multinomial Naive Bayes Classifier 스팸 메일 예제

위 그림과 같이 10개의 메일이 있습니다. 빨간색은 스팸이고 녹색은 정상 메일입니다.
- p(정상메일) = 6/10
- p(스팸메일) = 4/10

정상 메일을 열어서 확인해보니 안녕이라는 문구가 총 13번 그래라는 문구가 8번 광고라는 문구가 2번이라고 확인했습니다.
- p(안녕|정상메일)=13/23
- p(그래|정상메일)=8/23
- p(광고|정상메일)=2/23

광고 메일을 열어서 문구를 확인하니 위와 같았습니다.
- p(안녕|스팸메일)=1/13
- p(그래|스팸메일)=4/13
- p(광고|스팸메일)=8/13
Multinomial Naive Bayes Classifier 시작!
자!! 이제 Training Data로 위와 같은 값들을 얻었으니 스팸 메일을 구별 해보겠습니다.
메일이 들어 왔는데 "안녕"이 두 번 들어 있고 "그래"가 한번 들어 있는 메일입니다.
p(정상메일) x p(안녕|정상메일) x p(안녕|정상메일) x p(그래|정상메일) = 0.0666 ∝ p(정상메일|안녕 안녕 그래)
p(스팸메일) x p(안녕|스팸메일) x p(안녕|스팸메일) x p(그래|스팸메일) = 0.0007 ∝ p(스팸메일|안녕 안녕 그래)
위 두 확률 값을 비교해서 해당 메일이 정상메일일 확률이 높다는 사실을 알 수 있습니다.
Multinomial Naive Bayes Classifier : Laplace estimator
라플라스 추정치라고도 하고 Laplace Correction이라고도 합니다.
라플라스 추정치는 값이 없는 경우 예측에 오류가 발생하기 때문에 보정값으로 넣어줍니다. 예를 들어 앞서 예제에서 Training Data에서 "그래"라는 문구가 정상 메일에서 없는 경우 Likelihood 값을 구하면 항상 0이 나옵니다. 그러면 정상 메일의 경우도 무조건 스팸으로 판단하게 됩니다.
p(안녕|정상메일) x p(안녕|정상메일) x p(광고|정상메일) 의 경우 라플라스 추정치를 넣은 값은 아래와 같습니다.
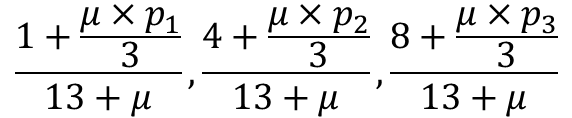
p1+p2+p3 =1 로 사용자가 원하는 가중치를 넣을 수 있습니다.
위와 같이 라플라스 추정치를 넣게 되면 0인 값을 보정해줄 수 있습니다.