FT(Fourier Transformer) 와 DTFT(Discrete time) 비교, 그래프와 수식으로 이해하기 (푸리에 vs 이산시간 푸리에변환)

FT(Fourier Transformer, 푸리에 변환) vs DTFT(Discrete Time Fourier Transformer, 이산 시간 푸리에 변환)

---

FT(Fourier Transformer, 푸리에 변환)와 DTFT(Discrete Time Fourier Transformer, 이산 시간 푸리에 변환) 결과 차이

 

1. x(t)라는 신호에 대해 푸리에 변환을 하고 X(ω)로 표기하자. 

2. x(t) 신호를 τ 시간 간격으로 샘플링을 하고 나온 그래프를 y(n) 이라고 하자. y(n) = x(n x τ)

3 . y(n)을 DTFT를 하여 나온 값을 Y(ω)로 표기하자. 

 

질문) 1~3번 과정을 통해서 x(t)라는 신호에서 FT를 이용해서 X(ω)와 샘플링과 DTFT를 이용해 Y(ω)를 구하였다. X(ω)과 Y(ω)는 유사할까?

 

정답) 그렇다. Y(ω) 는 X(ω)과 비교하여 크기가 변경되고(scaled) 반복되는(repeated) 형태의 그래프를 가진다. 

아래 그림은 나중에 나올 예제의 그래프인데 DTFT를 통해 나온 그래프가 FT와 유사한 형태임을 알수 있다. (scaled, repeated)

 

그림1 - x(t)

그림2 - y(n)

그림3 - X(ω)

그림4 - Y(ω)

 

 

---

FT(Fourier Transformer, 푸리에 변환)와 DTFT(Discrete Time Fourier Transformer, 이산 시간 푸리에 변환) 수식 전개

 

 

그림1

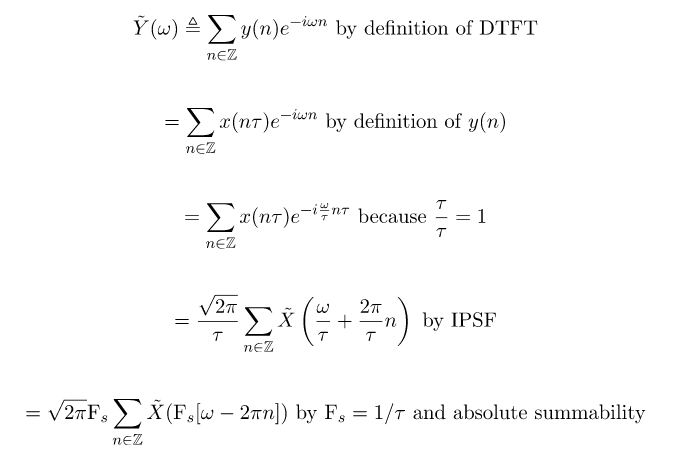
그림1은 y(n)을 DTFT 변환한 수식을 IPSF(Inverse Poisson Summation Formula)를 사용해서 X(ω) 관련 식으로 변환하는 과정이다.

 

최종 결과 수식을 통해 우리는 아래와 같은 특징을 알 수 있다.

 

DTFT의 특징

• X(ω)를 2 x fs(샘플링) 주기로 반복
• 주파수 축을 fs 배수로 좁혀줌
• 진폭을 √2𝜋fs 배수로 증가시켜줌

 

참조링크 >>

https://vru.vibrationresearch.com/lesson/the-dtft-of-a-sampled-sequency/