FFT(Fast Fourier Transform) - Sampling rate, Bandwidth, 측정시간, 주파수정밀도(resolution)
FFT(Fast Fourier Transform)란?
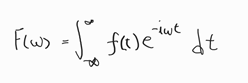
푸리에(Fourier) 변환을 수식으로 보면 그림1과 같다. 전 시간 영역을 적분하여 주파수 영역에 대한 수식으로 변환해주는 것이다. 푸리에 변환을 사용한다면 주파수 분석하고 싶은 신호를 다 받은 다음에 처리가 가능하다. 하지만 실시간으로 신호의 주파수 분석에 대한 요구가 생겼고 이를 가능하게 해주는 것이 FFT(Fast Fourier Transform) 이다.

실제로 실시간 분석은 아니고 아래 그림과 같이 시간(T)을 조각내서 주파수 분석을 올려준다. 빠른 컴퓨팅 기술을 사용해서 사용자는 마치 실시간과 같이 느끼게 되는 것이다. FFT는 그림1의 수식을 사용할 수 없어서 그림2와 같이 이산푸리에변환 식을 이용한다.

그림3에서 T는 frame이라고도 하고 buffer라고도 하는데 해당 시간만큼 잘라서 이를 FFT 변환을 통해 주파수로 변환해주는 것이다.
샘플링 rate, Bandwidth, 측정시간, 주파수정밀도(resolution) 사이 관계
- S(rate) / 2 = f(max) - 식(1)
1번 관계는 Nyquist 샘플링 이론에서 기안한것이다. 원주파수 모델을 재현하기 위해 최소한 2배의 샘플이 필요하다는 이론인데, 2배 또는 2.56 배를 사용한다.

그림4는 FFT 장비 설정화면인데 3200의 Sample rate(S(rate))를 사용하면 f(max)가 1250Hz로 고정됨을 알 수 있다. (3200/2.56 = 1250)
- Δt = S(rate) - 식(2)
- N = 2의 지수승 - 식(3)
- T = Δt x N = N/S(rate) - 식(4)
식(2)는 sampling rate는 샘플갯수(N)을 1초로 나눈 것이므로 역수는 샘플간의 시간 간격 Δt가 된다. 식(3)은 FFT의 특성과 관련있는 식으로 푸리에 변환과 근접한 결과를 얻기 위해서 샘플의 갯수(N)은 2의 지수승이여야 한다. 2, 4, 8, 16, 32 .... 와 같은 샘플 갯수를 가져야한다. 이유는 FFT 수식과 관련된 부분이라 자세한 이유는 몰라 생략하겠다.
- Δf = f(max)/(N/2) = S(rate)/N = 1/T - 식(5)
식(5)에서 샘플갯수(N)으로 나누지 않고 N/2로 나눈 이유는 그림2의 DFT(Discrete Fourier Transformer)와 관련 있다. 시간에서 N개의 샘플을 가져오면 주파수에서는 DFT에 의해 겹치는 주파수 성분이 2개씩 발생하고 그래서 N/2개의 성분이 주파수에서 남게 되는 것이다.
Trade off 관계

그림5는 FFT 분석에 사용하는 설정 화면이다. Number of lines 은 주파수 정밀도(Δf, Frequency resolution)과 관련 있다. 식(1)에서 f(max)를 몇 조각 낼지를 결정하는 것이다. 앞서 f(max)를 1250Hz로 정하였다. 1250hz / 1600개 (= 0.78125Hz) 로 조각 내므로 주파수 resolution이 0.78125hz가 된다.
식(5)에 따라 Δf를 작게 가져가서 resolution을 높일 수 있지만 그렇게 되면 T값이 증가한다. 위 설정에서 T 값은 1/0.78125 = 1.28초이다. 그리고 Δf 를 작게 가져가는 다른 방법은 f(max)를 줄이는 것인데 이는 FFT bandwidth가 줄게 되는 것이다. 그러므로 사용 조건에 따른 적절한 설정이 필요 하다.
'여러가지공부' 카테고리의 다른 글
| 오버샘플링(Oversampling)이란? (Fourier Transformer) (0) | 2021.05.29 |
|---|---|
| FT(Fourier Transformer) 와 DTFT(Discrete time) 비교, 그래프와 수식으로 이해하기 (푸리에 vs 이산시간 푸리에변환) (0) | 2021.05.28 |
| 확률분포함수, 누적분포함수, 가우시안분포란? 정말 쉬운 예제로 이해해보기(PDF, CDF, Gaussian) (0) | 2021.05.26 |
| 진동 시험 장비 절연 (Vibrator/Shaker Isolation) 방법 및 수식 정리 (0) | 2021.05.17 |
| 소리의 속도, 파장 길이, 주파수 관계와 각 분야별 진동 주파수 발생 범위 (0) | 2021.05.14 |