Stress - Life 그래프
앞에 "Stress - Life 그래프란(1)? (SN 그래프)" 포스트 이후 계속 정리하겠다 "Stress - Life 그래프란(2)? (SN 그래프)"는 아래 링크를 참조 하길 바랍니다.
링크 : scribblinganything.tistory.com/122

평균 응력 효과 (Mean Stress Effects)
실험실에서 수집된 대부분의 기본 S-N 피로 데이터는 "reversed stress cycle"을 사용하여 생성된다. "reversed stress cycle" 는 응력이 양수와 음수 크기로 왔다갔다하는 것이다. 그러나 실제 하중 적용에는 아래 그림과 같이 진동 응력이 중첩되는 평균 응력이 수반된다(양수 측에서만 동작). 다음 정의는 교대(alternating) 및 평균(mean) 응력이 모두 있는 스트레스 주기를 정의하는 데 사용됩니다. 응력 범위는 사이클의 최대 응력과 최소 응력 사이의 차이입니다. 응력은 그리스어 감마로 표현한다.

응력 진폭(amplitude)은 응력범위의 반이다.

mean stress 는 최대 최소 응력의 평균 값이다.

진폭 비율 (amplitude ratio) A는 아래와 같이 표현 된다.
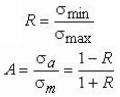

완전 "reversed stress cycle" 조건의 경우 R은 -1과 같습니다 양과 음이 같은 크기의 진폭을 가지기 때문입니다. 정적 로드의 경우 R은 1과 같습니다. 평균 응력이 응력 진폭과 같은 경우 R은 0입니다(스프링처럼 같은 힘으로 댕겼다가 복귀). R 0.1의 응력 주기는 항공기 구성요소 시험에 종종 사용되며, 최소 응력이 최대 응력의 0.1배인 장력-장력 주기에 해당한다.
0이 아닌 평균 응력을 사용한 피로 테스트의 결과는 아래 그림과 같이 "Haigh diagram"으로 나타낸다. "Haigh diagram"은 X축을 따라 평균 응력, Y축을 따라 진동 응력 진폭을 나타낸다. 상수 수명 선(Lines of Constant Life)은 데이터 점을 통해 그려집니다. 무한 수명 영역은 곡선 아래의 영역이고 유한 수명 영역은 곡선 위의 영역입니다. 유한 수명(Finite life)에서 내구성 한계(endurance limit)은 Mean stress가 0이고 R = -1인 "reversed stress cycle" 와 같다. 왜냐하면 SN 그래프는 "reversed stress cycle" 를 기초로 만들었기 때문이다.
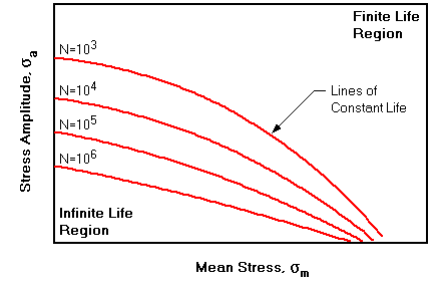
위 그림과 같은 Haigh diagram"을 생성하려면 매우 많은 양의 테스트가 필요하며, 평균과 교대 응력의 모든 조합에 대한 곡선을 개발하는 것은 일반적으로 비현실적이다. 이러한 어려움을 해결하기 위해 교대 스트레스를 평균 스트레스와 연관시키는 몇 가지 경험적 관계가 개발되었다. 아래 수식들은 경험적 관계를 정립한 내용들이다.
Sy : Yield Strength
Su : Ultimate Strength
Se : Endurance limit
감마f : fracture stress

위 수식을 그래프로 변환한것은 아래 그림과 같다. 가장 많이 사용되는 수식은 Goodman과 Gerber 수식이다. 수많은 테스트 결과를 통해 대부분은 위 두식 사이에 그래프를 형성한다. Goodman은 수학적으로 단순함과 수치가 보수적이라는 장점이 있다.

위 그림에서 Se는 Endurance limit, Sy는 Yield strength (내부에 변형 발생하지않고 돌아가는 힘), Su는 Ultimate strength (Stress-Strain 그래프에서 Stress가질 수 있는 최대값), 감마f는 fracture strength( Stress-Strain 그래프에서 망가질때 strength)이다. 한가지 알아야할 부분은 Se만 amplitude 이고 나머지는 mean 값이다.
아래 규칙은 수식들에 적용되는 룰들이다.
- "tensile" 평균 응력 값을 사용해야한다.
- 평균 응력(stress)가 아주 작은 값일 경우 "alternating stress(R = -1)" 와 큰 차이가 없다.
- Soderberg 방식이 가장 보수적인 접근이다.
- 단단한 금속(취성, brittle)의 경우 Goodman과 Morrow 그래프의 ultimate strength는 true fracture stress 에 근접한다.
- R이 1에 가까워질 수 록 위 수식들과 괴리가 발생한다. (진폭이 거의 없음)
Notches (흠집)
앞서 설명한 그래프나 이론들은 테스트 하는 재료에 흠집이 없는 이상적인 상태를 가정해서 진행한 것이다. 하지만 현실에서는 fatigue failure 가 발생하는 지점은 흠집(notch)이나 응력(stress)가 집중 되는 부분이다.
거의 모든 기계 부품과 구조 부재는 어떤 형태의 기하학적 또는 미세 구조 불연속성의 특성을 지닌다. 이러한 불연속성(discontinuities) 또는 응력 집중 계수(stress concentration factors)는 종종 부재의 일반적인(nominal) 응력 S보다 몇 배 더 큰 최대 지역 응력 Smax를 만들어낸다. 이상적으로 탄성(elastic) 부재에서 이러한 응력의 비율은 아래 수식으로 표현된다. Kt는 stress concentration factor 이다.

이론적 응력 집중 계수(tress concentration factor)는 기하학 및 하중 모드(축, 평면 내 굽힘 등)에의해 결정된다.
Stress-Life 그래프에서 Notch의 효과는 피로 노치 계수 Kf(피로 스트레스 집중 계수라고도 함)에 의해 설명된다. 피로 노치 계수는 노치없는 이상적인 재료의 피로 강도(철금속 내구성 한계)와 노치 피로 강도와의 비율이다. 아래 식을 참조하자

대부분의 경우 fatigue notch factor는 stress concentration factor 보다 작다.

추가적인 효과를 표현하기 위해 notch sensitivity factor q 를 아래와 같이 만들었다.

q 값의 범위는 0(노치 효과 없음, Kf = 1)에서 1(완전한 이론적 효과, Kf = KT)입니다. 많은 연구자들은 실험 데이터에 대한 상관 관계를 바탕으로 q의 결정을 위한 분석 관계를 제안했다. 가장 흔한 관계는 Peterson과 Neuber가 제안한 관계이다. Peterson과 Neuber 관계는 모두 데이터에 대한 경험적 곡선 적합이다. 분석에 사용할 경우 접근 방식에는 거의 차이가 없습니다. 두 방법 모두 q가 재료, 노치 형상 및 노치 크기와 관련이 있음을 보여줍니다. 따라서 두 노치는 q 값이 다르기 때문에 KT 값은 동일하지만 Kf 값은 다를 수 있습니다. 두 가지 접근 방식 모두 다음과 같습니다.
Kf에 대한 제한값을 지지한다. 제한 값은 재료에 따라 다르지만 일반적으로 5와 6 사이입니다.
Peterson 방정식에 따른 notch factor sensitivity는 아래와 같다.

r: notch의 radius, a는 재료가 가지는 상수값
상수 a는 재료 강도와 연성(ductility)에 따라 달라지며, notch 있는 경우와 없는 모든 경우에 대해 피로 시험을 통해 실험적으로 얻어진다. 단단한 금속의 날카롭게 파인 notch는 notch 민감도가 높은 경향이 있다.
철 기반 가공 금속은 다음과 같이 상수 a 를 가진다.

Neuber 방정식에 따른 notch factor sensitivity는 아래와 같다.

r: notch의 radius, p: 재료가 가지는 상수 (재료 내부 알갱이(grain) 크기와 관련)
notch factor Kf는 notched 된 재료의 fatigue strength를 교정할때 사용함

Kf를 SN 그래프 교정을 위해 사용하면 결과는 보수적으로 변한다.
'여러가지공부' 카테고리의 다른 글
| SDOF(Single degree of freedom)에서 Mass-Spring-Damper 이해하기 (1) | 2021.04.06 |
|---|---|
| FRF (Frequency Response Function, 주파수 응답)이란? (0) | 2021.04.05 |
| Stress - Life 그래프란(1)? (SN 그래프) (0) | 2021.01.29 |
| 피로도(fatigue)란? 재료 특성(Material Properties), 환경 로드(Loading), 기하학(Geometry)구조에 따른 피로도 계산 방법 (0) | 2021.01.27 |
| 내구성 (Durability) 이란? 설계 시 고려할 점은? (0) | 2021.01.26 |