목차

파이썬 Gradient Descent란?
선형 회기(Linear Regression)는 데이터 셋(Data set)을 대표하는 하나의 선을 구하는 작업이었습니다. 즉, Y = a x X + b에서 기울기 값 a와 절편 값 b를 구하였습니다. 이때 사용된 방식은 RSS(Residual Sum of Squares)이었습니다. 잔차 제곱 방식라고 불리는 예측되는 선형회기 선과 실제 데이터 셋의 제곱 합이 최소가 되게 만드는 선형회기 선을 만드는 작업입니다.

그림에서 파란색선의 제곱의 합을 RSS(Residual Sum of Squares)라고 하고 RSS(Residual Sum of Squares)가 가장 작은 지점의 기울기와 절편을 구하는 알고리즘은 OLS(Ordinary Least Sqaures)라고 합니다.
Gradient Descent란?
Gradient Descent / Steepest Descent 는 머신러닝(Machine Learning)의 선형 회기(Linear Regression)에서 가장 많이 사용되는 알고리즘 중에 하나 입니다.
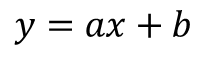
알고리즘의 목적은 데이터 셋을 대변하는 수식 1의 절편과 기울기를 구하는 것입니다. 여기서 Loss 또는 Cost Function이라는 함수가 필요 합니다.

Gradient Descent는 위 그림과 같이 Cost Function이 최소가 되는 기울기와 절편을 찾는 과정입니다. Cost Function은 여기서 MSE(Mean Squared Error) 수식을 사용 했습니다(수식2 참조). 앞서 RSS(Residual Sum of Squares)의 데이터셋을 나눠준 개념입니다.

위 이미지 처럼 기울기 a와 절편 b를 Cost Function이 작아지는 지점으로 이동하면서 a, b를 찾는 알고리즘을 Gradient Descent 라고 합니다.
SGDRegressor Syntax (파라미터 설정)
class sklearn.linear_model.SGDRegressor(loss='squared_error', *, penalty='l2', alpha=0.0001, l1_ratio=0.15, fit_intercept=True, max_iter=1000, tol=0.001, shuffle=True, verbose=0, epsilon=0.1, random_state=None, learning_rate='invscaling', eta0=0.01, power_t=0.25, early_stopping=False, validation_fraction=0.1, n_iter_no_change=5, warm_start=False, average=False)
SGDRegressor는 Stochastic Gradient Descent 알고리즘으로 Gradient Descent 에서 모든 값을 대입해서 기울기를 찾는 방식이 아닌 하나의 시작점에서 기울기를 찾는 방법으로 속도가 빠른 장점이 있습니다.
Syntax는 위와 같이 다양하게 있는데 이 중에 가장 많이 사용하는 파라미터는 아래와 같습니다.
- max_iter
- eta0
- random_state
max_iter 의 범위는 1에서 무한대입니다. Training Data를 검토하는 최대 횟수를 의미합니다. max_iter를 키울 수록 앞서 Cost Function을 최소로 가져갈 확률이 높아 집니다.
eta0 은 Learning rate라고 합니다. 앞서 경사와 Loss를 나타낸 그래프에서 경사값을 변경하는 크기라고 생각하시면 됩니다. 범위는 0에서 무한대 입니다.
random_state는 Train, Test model 형성을 위해 가져올 때 사용되는 Random seed라고 생각하시면 됩니다. random_state를 동일한 값으로 설정하면 값을 가져오는 랜덤 순서도 동일합니다.
파이썬 Stochastic Gradient Descent 실습하기
전체 코드>>
from sklearn.linear_model import LinearRegression, SGDRegressor
import matplotlib.pyplot as plt
import pandas as pd
from numpy import random
data_set = []
y_list = []
for _ in range(50):
x_val = random.randint(1,10)
mul = random.uniform(0.7,1.2)
y_val = x_val*mul
data_set.append([x_val, y_val])
df=pd.DataFrame(data_set, columns=['x_value','y_value'])
x = df.iloc[:, :-1].values
y = df.iloc[:, -1].values
L_reg = LinearRegression()
L_reg.fit(x, y)
L_y_pre = L_reg.predict(x)
S_reg0 = SGDRegressor(max_iter=10, eta0=1e-4)
S_reg0.fit(x, y)
S_y_pre0 = S_reg0.predict(x)
S_reg1 = SGDRegressor(max_iter=1000, eta0=1e-4)
S_reg1.fit(x, y)
S_y_pre1 = S_reg1.predict(x)
#그래프 그리기
plt.title('Regression')
plt.xlabel('x value')
plt.ylabel('y value')
plt.scatter(x, y)
plt.plot(x, L_y_pre, color='red')
plt.plot(x, S_y_pre0, color='yellow')
plt.plot(x, S_y_pre1, color='green')
plt.show()
결과>>

Iteration이 10번으로 작은 노란색 그래프는 기울기 위치를 찾기 전에 모델 학습이 멈춰서 적절하지 못한 기울기를 나타내고 있습니다.
주석>>
data_set = []
y_list = []
for _ in range(50):
x_val = random.randint(1,10)
mul = random.uniform(0.7,1.2)
y_val = x_val*mul
data_set.append([x_val, y_val])
df=pd.DataFrame(data_set, columns=['x_value','y_value'])50개의 데이터 셋을 랜덤으로 생성 합니다.
L_reg = LinearRegression()
L_reg.fit(x, y)
L_y_pre = L_reg.predict(x)
S_reg0 = SGDRegressor(max_iter=10, eta0=1e-4)
S_reg0.fit(x, y)
S_y_pre0 = S_reg0.predict(x)
S_reg1 = SGDRegressor(max_iter=1000, eta0=1e-4)
S_reg1.fit(x, y)
S_y_pre1 = S_reg1.predict(x)형성된 데이터셋을 Linear Regression 모델과 SGD 모델로 만들어 냅니다. SGD는 파라미터 비교를 위해 max_iter 값을 다르게 설정하였습니다. S_reg0은 10번의 시행만을 진행하였으므로 기울기가 이상적인 위치를 찾기 전에 멈출 확률이 높습니다.
#그래프 그리기
plt.title('Regression')
plt.xlabel('x value')
plt.ylabel('y value')
plt.scatter(x, y)
plt.plot(x, L_y_pre, color='red')
plt.plot(x, S_y_pre0, color='yellow')
plt.plot(x, S_y_pre1, color='green')
plt.show()선형 회기 모델들의 비교를 위해 matplotlib으로 그래프를 그려 줍니다.
'파이썬(Python) > 머신러닝(Machine Learning)' 카테고리의 다른 글
| [Python] sklearn 정규 분포 만들기(StandardScaler), 그래프 비교 (0) | 2023.02.16 |
|---|---|
| [Python] sklearn 파이프라인(Pipeline) + ColumnTransformers (0) | 2023.02.14 |
| [Python] sklearn ColumnTransformer이란? 예제 실습(SimpleImputer, fit_transform) (0) | 2023.02.07 |
| [Python] sklearn train_test_split 사용법, Syntax, 예제 (0) | 2023.01.05 |
| [Python] sklearn 설치 및 기본 회귀 모델 예제 실습(Linear Regression) (0) | 2022.12.31 |