목차

엔트로피(Entropy)란?
엔트로피는 머신러닝에서 데이터셋의 불확실성을 나타내는 척도입니다. 엔트로피를 계산하기 위해서는 데이터셋에서 각 클래스가 발생할 확률을 알아야 합니다.
수식으로 표현하면 다음과 같습니다.
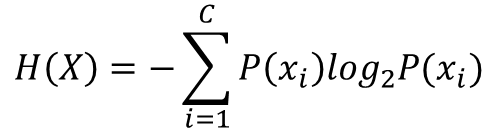
여기서 H(X)는 데이터셋 X의 엔트로피를 나타내며, p(x)는 데이터셋 X에서 클래스 x가 발생할 확률을 나타냅니다.
이 식은 다음과 같이 해석할 수 있습니다. 데이터셋에서 각 클래스가 발생할 확률을 곱한 후, 이를 로그로 변환하고 음수로 바꾼 값들을 모두 더한 것입니다.
수식1에서 log2를 사용하는 이유는 확률의 특성과 관련이 있습니다.
우선, 확률은 항상 0과 1 사이의 값을 가집니다. 하지만, 이러한 확률을 곱하면 값이 매우 작아질 수 있습니다. 예를 들어, 0.001과 0.0001을 곱하면 0.0000001이 됩니다. 이렇게 되면 컴퓨터에서는 부동소수점(float) 오차가 발생할 가능성이 높아집니다.
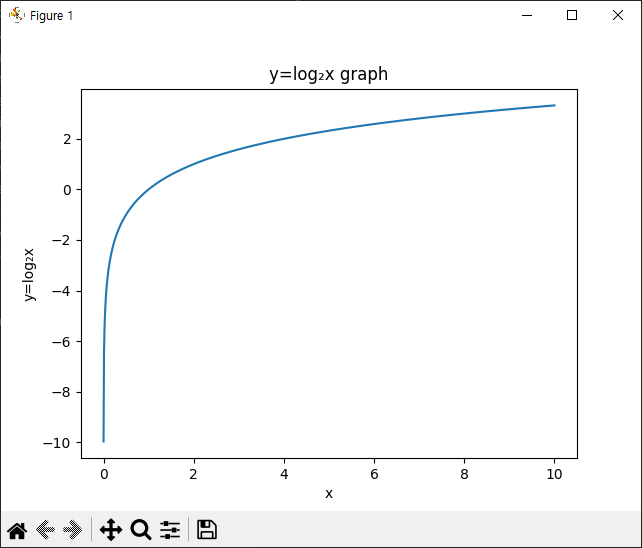
로그를 취하면 이러한 문제를 해결할 수 있습니다. 로그는 값을 작게 만들어줍니다. 예를 들어, log₂ 0.001은 -9.97이 되므로 매우 작은 값이 됩니다. 로그를 취하면 확률 곱셈을 덧셈으로 바꿀 수 있으므로, 컴퓨터에서 덧셈 오차가 발생하는 것보다 더 정확한 값을 계산할 수 있습니다. 그림처럼 0에 가까울 수록 로그 그래프는 마이너스로 커집니다.
또한, 로그를 사용하면 확률의 곱셈이나 나눗셈을 덧셈이나 뺄셈으로 바꿀 수 있습니다. 이는 수학적으로 계산하기 쉬워지므로, 엔트로피나 정보 이득(Information Gain) 등의 개념을 계산할 때 매우 편리합니다.
따라서, 머신러닝에서는 로그를 사용하여 확률을 처리하는 것이 일반적입니다. 엔트로피를 계산하는 식에서도 로그를 사용하는 이유는, 각 클래스가 발생할 확률의 곱을 더하기보다는 로그를 취한 값들을 더하는 것이 더욱 정확하고 효율적이기 때문입니다.
엔트로피(Entropy) 예제
예를 들어, 야구 경기에서 타자가 스윙을 치는 경우, 그 결과는 안타(Hit)와 아웃(Out) 두 가지 중 하나가 될 수 있습니다. 타자의 스윙 결과를 예측하는 모델을 만들기 위해, 이전의 타자들의 기록을 수집한 데이터셋이 있다고 가정해봅시다. 이 데이터셋은 다음과 같습니다.
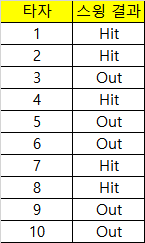
이 데이터셋에서, 엔트로피를 계산하려면 먼저 각 클래스(안타, 아웃)가 발생한 비율을 계산해야 합니다. 여기서는 안타와 아웃 두 클래스가 있으므로, p(Hit)와 p(Out)은 각각 0.4과 0.6이 됩니다.
그리고 이를 엔트로피 식에 대입하면 다음과 같이 계산됩니다.
H = - (0.4 * log₂ 0.4 + 0.6 * log₂ 0.6) = 0.97
즉, 이 데이터셋의 엔트로피는 약 0.97이 됩니다. 이 값은 데이터셋이 다소 불균일하다는 것을 나타냅니다.
이제, 이 데이터셋을 기반으로 결정 트리를 구성한다면, 각 노드에서는 엔트로피를 계산하여 최소화하는 방향으로 진행됩니다. 예를 들어, 루트 노드에서는 전체 데이터셋의 엔트로피를 계산하고, 이를 최소화하는 분할 방법을 선택합니다. 이후, 하위 노드에서도 동일한 방법으로 엔트로피를 계산하여 트리를 구성해나갑니다.
이렇게 결정 트리를 구성하는 과정에서 엔트로피는, 데이터셋의 불확실성을 나타내는 중요한 척도로 사용됩니다.
파이썬(Python) 예제 실습#1
이번 예제는 2가지 클래스에 대한 엔트로피를 그래프로 보여주는 파이썬 코드 입니다. 간단하게 설명드리면 동전을 던졌는데 앞면이 나올 확률이 0~1에 대해서의 엔트로피를 보여주는 것입니다.
예제 코드>>
import numpy as np
import matplotlib.pyplot as plt
# Define the range of probability values
p = np.linspace(0.01, 0.99, 100)
# Calculate the entropy values for each probability value
H = -p*np.log2(p) - (1-p)*np.log2(1-p)
# Plot the entropy values against the probability values
plt.plot(p, H)
plt.xlabel('Probability')
plt.ylabel('Entropy (bits)')
plt.title('Entropy vs. Probability')
plt.show()5번 라인: 확률값 0과 1은 8번 라인의 식에서 처리가 안되므로 0.01~0.99 확률로 설정하였습니다.
8번 라인: 2가지 경우에 대한 엔트로피 계산식입니다.
결과>>
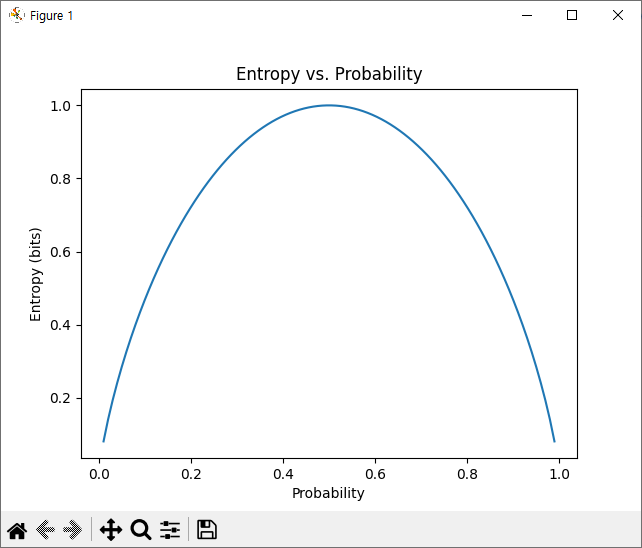
확률이 0이거나 1이 된다는 의미는 정보로서 의미가 없다는 뜻입니다. 그러므로 entropy가 0으로 나옵니다. 그리고 둘 중에 어떤 값이 나올지 모르는 0.5의 확률에서 엔트로피 값이 최대값 1이 나옵니다.
파이썬(Python) 예제 실습#2
이번 예제는 A, B, C라는 세가지 클래스를 10번 사건(event)에 대해 정의하고 각 클래스가 발생할 확률을 구해서 엔트로피를 계산하는 예제 입니다.
예제 코드>>
import math
# 데이터셋
dataset = [('1', 'A'),
('2', 'A'),
('3', 'B'),
('4', 'C'),
('5', 'B'),
('6', 'C'),
('7', 'A'),
('8', 'B'),
('9', 'C'),
('10', 'C')]
# 클래스(사건)의 개수
num_classes = len(set([data[1] for data in dataset]))
# 각 클래스(사건)의 발생 빈도 계산
class_freq = {}
for data in dataset:
class_name = data[1]
if class_name in class_freq:
class_freq[class_name] += 1
else:
class_freq[class_name] = 1
# 각 클래스(사건)의 발생 확률 계산
class_prob = [freq / len(dataset) for freq in class_freq.values()]
# 엔트로피 계산
entropy = -sum([prob * math.log2(prob) for prob in class_prob])
print('Entropy:', entropy)
결과>>
Entropy: 1.5709505944546684
'여러가지공부 > 머신러닝(Machine Learning)' 카테고리의 다른 글
| [머신러닝]민감도, 특이도, F1-Score란?(Sensitivity, Specificity) (0) | 2023.04.03 |
|---|---|
| Classification 모델 성능 검증: Accuracy, Precision/Recall, ROC-AUC(예제 실습, 파이썬) (0) | 2023.04.03 |
| [머신러닝] k-fold cross validation이란? 파이썬 예제 실습 (0) | 2023.03.31 |
| [머신러닝] 편형(Bias)와 분산(Variance)란? 파이썬 예제 코드로 이해하기(Trade off) (0) | 2023.03.31 |
| [머신러닝]일반화(Generalization), 과적합(Overfitting, Underfitting)이란? 파이썬 코드 예제(그래프 포함) (0) | 2023.03.30 |