[Python]지수 분포란? 파이썬으로 구현하고 그래프 만들기(Exponential Distribution)

 

목차

 

 

 

 

지수 분포란(Exponential Distribution)?

 

지수 분포는 푸아송 분포와 연결해서 생각할 수 있습니다. (아래 링크 참조)

[Python]푸아송 분포란? 파이썬으로 구현하고 그래프 그리기(Poisson distribution) (tistory.com)

 

푸아송 분포는 간단하게 설명하면 λ = np를 사용해서 n번 시행하니 p의 확률이 발생했다는 비율을 사용해서 분포를 구하는 것입니다. 즉, 단위 시간당 n 번 발생 확률(Probability)을 이용해서 분포를 구성하는 것이고 지수 분포는 어떤 사건이 발생하기 까지의 시간의 확률로 분포를 만든 것입니다.

 

예를 들어 A는 매일 커피를 3잔 씩 마실 확률이 0.5면  λ(람다)값은 1.5가 되고 람다 값으로 발생률에 따른 푸아송 분포를 알수 있습니다. 푸아송 분포의 람다값을 사용해서 다음 번에 커피 마실때까지 걸리는 시간을 지수 분포로 구할 수 있는 것 입니다.

 

By Newystats - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=80359746

By Skbkekas - Own work, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=9508326

 

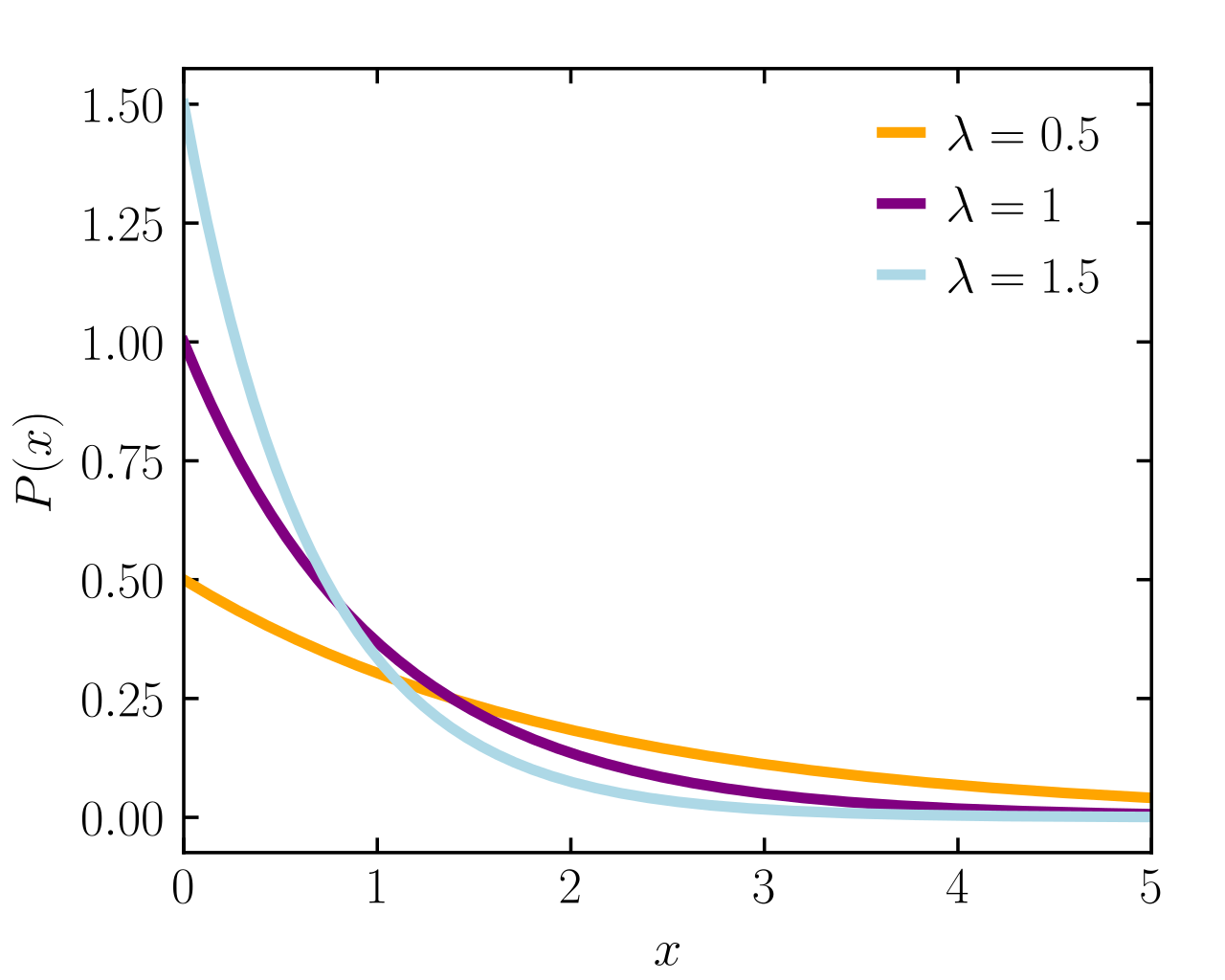
위 그림은 지수 분포의 확률 밀도 함수(PDF, Probability Density Function)과 누적 확률 밀도함수(CDF, Cumulative distribution function)의 그림입니다. 

 

CDF 그래프에서 람다가 1.5일때 x가 3인 3일 내에 커피를 마실 확률은 거의 1에 가까워 집니다.

 

PDF 수식과 CDF 수식은 아래와 같습니다.

PDF, wiki

CDF, wiki

 

람다 값에 따라 지수적인 분포를 가짐을 알 수 있습니다.

 

 

파이썬으로 구현하기

 

python의 numpy(넘파이)의 랜덤의 exponential 함수를 사용하면 쉽게 분포를 사용하는 값을 불러 올 수 있습니다.

 

입력값으로는 scale과 size를 받습니다. scale은 람다 값의 역수 베타(b)이고 size는 몇 개의 값을 부를지를 선택 합니다.

 

예제 코드>>

from numpy import random

x_list = random.exponential(scale=0.67, size=10)

print(x_list)

3번 라인: 앞서 커피 예제 처럼 1.5 람다 값을 사용해서 1/1.5 =0.67입력 합니다. 그리고 총 10개의 값을 불러 옵니다.

 

결과>>

[0.68480154 1.09794309 0.26246966 1.87275596 0.78829701 0.18395959
 0.19972253 0.25537992 0.80447547 0.02605827]

 

 

 

파이썬으로 그래프 그리기

 

그래프로 위키피디아에서 지수분포의 PDF 그래프로 유사하게 나오게 하기 위해서는 size를 키워야 합니다. 이번 예제에서는 10000개의 사이즈로 그래프를 그려 보겠습니다.

 

예제 코드>>

from numpy import random

x_list = random.exponential(scale=0.67, size=10)

# print(x_list)

import matplotlib.pyplot as plt
import seaborn as sns

sns.displot(x_list, kind="kde")
plt.show()

7~11번 라인: 확률 밀도 함수를 그리기 쉽게 도와주는 seaborn이라는 라이브러리를 사용합니다.

 

결과>>

앞서 1.5lamda값을 가지는 PDF와 유사하게 나왔습니다.