목차

로지스틱 분포, 로지스틱 함수, 로지스틱 회귀란?


위 그림은 위키피디아에서 가져온 로지스틱 분포(Logistic distribution)의확률 밀도 함수(Probability density function)과 누적 분포 함수(Cumulative distribution function)의 그래프입니다. 그림을 참조하면 로지스틱에 대해 쉽게 이해할 수 있습니다.
로지스틱 분포(Logistic distribution)란?
세상의 현상은 선형(Linear)보다는 지수적(Exponential)으로 발생하는 일들이 많습니다. 가령 자동차를 예를 들면 사용 시간에 따른 차량이 고장날 확률을 생각할 경우 결과를 정상과 고장 두가지로 봤을 때 어느 시점에 고장 발생활률이 높게 증가함을 통계를 통해 알 수 있습니다.
이러한 현상을 표현 한 것이 두번째 그림입니다. u는 location 파라미터이고 확률 밀도에서 평균에 상응하는 값입니다. s는 scale로 표준편차(Standard deviation)에 사응하는 결과 입니다.
앞서 자동차의 예를 들면 u=5, s= 2는 5년 시점에 고장 확률이 급격하게 증가하고 증가 비율은 s=2를 따르는 것 입니다.
로지스틱 함수(Logistic function), 로지스틱 회귀(Logistic regression)란?
앞서 분포를 이해하셨다면 함수와 회귀는 같은 개념에서 설명 드릴 수 있습니다. 분포를 만들어주는 수식을 로지스틱 함수라 부를 수 있고 회귀란 함수의 값을 끝과 끝으로 보내면 특정 값으로 회귀를 하기 때문에 붙여진 이름입니다. 앞서 자동차의 예에서 시간이 무한대로 지나면 결국 고장이라는 결과로 회귀하게 되는 것입니다. 그리고 시간을 0으로 보내면 결과는 정상으로 회귀하게 됩니다.
로지스틱 분포 수식
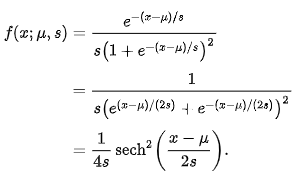
CDF

로지스틱 분포 파이썬(Python)으로 구현하기
로지스틱 분포를 사용하기 위해 파이썬의 넘파이/넘피(Numpy)를 이용합니다. 넘파이 랜덤에서 logistic 함수를 사용하면 logistic 분포를 사용하는 값을 불러 올 수 있습니다. 입력 값은 아래와 같습니다.
- loc : location 값
- scale : scale 값
- size : 뽑을 데이터 개수
코드>>
from numpy import random
x_list = random.logistic(loc=5, scale=2, size=20)
print(x_list)
결과>>
[ 6.25541922 1.77802012 10.20794159 12.87644676 2.58512724 5.56115649
4.68609139 5.84809371 1.06521357 0.67986838 2.79811446 8.12281955
7.19264311 5.96181359 7.9041748 0.97389994 -0.47236753 5.43133782
2.82645199 5.27896018]
로지스틱 분포 그래프 그리기
코드>>
from numpy import random
x_list = random.logistic(loc=5, scale=2, size=20)
print(x_list)
import matplotlib.pyplot as plt
import seaborn as sns
sns.displot(x_list, kind="kde")
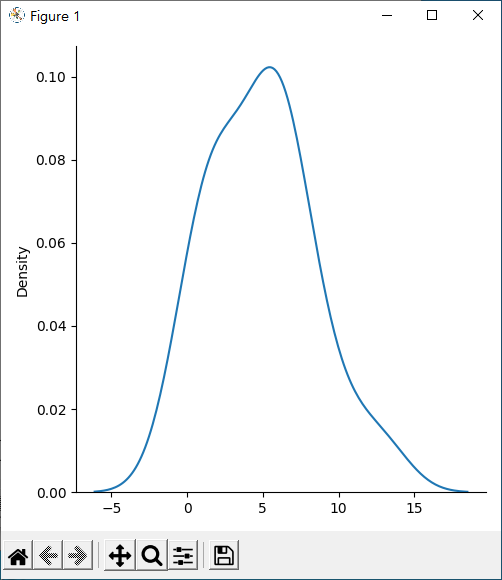
plt.show()앞서 코드에7~11번 라인만 추가하면 됩니다. seaborn은 파이선의 그래프 그리는 도구로 kde를 사용하면 선 형태로 그려 줍니다.
결과>>
'파이썬(Python) > numpy' 카테고리의 다른 글
| [Python]No module named numpy 관련 에러 해결 방법 (0) | 2022.02.04 |
|---|---|
| [Python]지수 분포란? 파이썬으로 구현하고 그래프 만들기(Exponential Distribution) (0) | 2022.01.27 |
| [Python]푸아송 분포란? 파이썬으로 구현하고 그래프 그리기(Poisson distribution) (0) | 2022.01.20 |
| [Python] 균등분포 란? 파이썬으로 구현하고 그래프 만들기(Uniform Distribution) (0) | 2022.01.19 |
| [Python]이산 확률 분포란? 파이썬으로 구현하고 그래프로 그리기(Binomial/Discrete) (0) | 2022.01.18 |